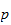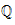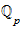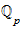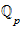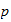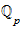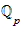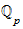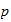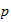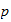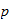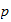Informationen zum Proseminar
Einführung in die p-adische Analysis
Sommersemester 2015
Dozentin: Prof. Dr. Annette Huber-Klawitter
Tutorium: Dr. Oliver Bräunling
Termine
- wir beginnen gleich in der ersten Woche der Vorlesungszeit, also am 21.4.2015.
- Zeit und Ort des Proseminars: Di 12-14, SR 404, Eckerstr. 1
Studien/Prüfungsleistung
- Studienleistung: regelmäßige Teilnahme
- Prüfungsleistung: Halten eines Vortrags
Achtung: Es gibt eine schon mehrfach aufgetretene Quelle der Verwirrung: Die Seitenangaben im Programm zum Buch von Gouvea beziehen sich auf die zweite Auflage. Über die Uni-Rechner ist diese Auflage als e-book verfügbar:
Springer E-book (nur über die Uni-Rechner aufrufbar).
Unsere Bibliothek hat das Buch auch in Papierform, allerdings nur in der ersten Auflage. Tatsächlich erscheinen die Unterschiede im Text eher gering, allerdings sind die Seitenzahlen geringfügig verschoben.
Generell ist es sicher eine gute Idee, sich eher an die zweite Auflage zu halten, schließlich bedankt sich Gouvea im Vorwort für all diejenigen, die ihn auf Druckfehler in früheren Drucken aufmerksam gemacht haben.
Programm
Einführung in die p-adische
Analysis
Ankündigung:
Dieses Proseminar verknüpft Analysis und Zahlentheorie. Die Analysis
fußt ganz wesentlich auf dem Begriff der
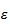 -Umgebung
-Umgebung
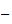 Zahlen sind \nah", wenn ihre Differenz einen kleinen Betrag hat. Man kann
allerdings auch ganze Zahlen \nah" nennen, wenn ihre Differenz durch eine hohe
Potenz einer Primzahl
Zahlen sind \nah", wenn ihre Differenz einen kleinen Betrag hat. Man kann
allerdings auch ganze Zahlen \nah" nennen, wenn ihre Differenz durch eine hohe
Potenz einer Primzahl
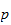 teilbar ist. Ähnlich wie die reellen Zahlen aus den rationalen entstehen,
indem man fordert, dass alle Cauchyfolgen konvergieren sollen, kann man die
rationalen Zahlen auch erweitern, indem man dasselbe für diesen
völlig anderen Begriff von
teilbar ist. Ähnlich wie die reellen Zahlen aus den rationalen entstehen,
indem man fordert, dass alle Cauchyfolgen konvergieren sollen, kann man die
rationalen Zahlen auch erweitern, indem man dasselbe für diesen
völlig anderen Begriff von
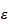 -Umgebung
fordert. Und genau dies sind die berühmten
-Umgebung
fordert. Und genau dies sind die berühmten
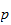 -adischen
Zahlen. Es gibt Folgen, die nicht in den reellen Zahlen konvergieren, aber in
den
-adischen
Zahlen. Es gibt Folgen, die nicht in den reellen Zahlen konvergieren, aber in
den
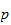 -adischen
-adischen
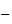 und sogar Folgen, die sowohl
und sogar Folgen, die sowohl
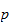 -adisch
wie auch reell konvergieren, aber mit unterschiedlichen Grenzwerten.
-adisch
wie auch reell konvergieren, aber mit unterschiedlichen Grenzwerten.
Ein Großteil der klassischen Analysis lässt sich auch für die
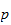 -adischen
Zahlen entwickeln, und sehr vieles ist ganz ähnlich zur üblichen
Analysis, und gleichzeitig doch auch ganz anders. Man muss sich selbst damit
beschäftigen, um diese spannenden Phänomene wirklich verstehen zu
können. Und genau dies wollen wir in diesem Proseminar tun.
-adischen
Zahlen entwickeln, und sehr vieles ist ganz ähnlich zur üblichen
Analysis, und gleichzeitig doch auch ganz anders. Man muss sich selbst damit
beschäftigen, um diese spannenden Phänomene wirklich verstehen zu
können. Und genau dies wollen wir in diesem Proseminar tun.
Vorbesprechung:
Montag, 9. Februar 2015, 10-12 Uhr, Besprechungsraum Stochastik 10-12 Uhr
Anmeldung:
Teilnehmer-Liste bei Frau Frei (Raum 433)
Literatur:
Gouvea, Fernando Q. p-adic numbers. An introduction.
Second edition. Universitext. Springer-Verlag, Berlin, 1997
Unsere Bibliothek hat diese Auflage als e-book; in Papierform nur die erste Auflage (Achtung: leicht verschobene Seitenzahlen).
Robert, Alain M. A course in p-adic analysis. Graduate
Texts in Mathematics, 198. Springer-Verlag, New York, 2000
Koblitz, Neal p-adic numbers, p-adic analysis, and
zeta-functions. Second edition. Graduate Texts in Mathematics, 58.
Springer-Verlag, New York, 1984
Wir werden hauptsächlich dem Buch von Gouvea
folgen.
Ablauf:
-
Je nach Teilnehmerzahl sollen die Vorträge einzeln oder zu zweit
vorbereitet und gehalten werden, wobei die Themen gleichmäßig
aufgeteilt werden sollen.
-
Alle Vortragenden sollten mindestens eine Woche vor ihrem Vortragstermin zu
einer Vorbesprechung kommen, zu der der Vortrag bereits vollständig
ausgearbeitet sein soll.
-
Die Vorträge sollen ca.
80 Minuten lang sein. Man sollte dabei beachten, dass Zwischenfragen der
Zuhörer erlaubt und auch erwünscht sind, sodass man effektiv
deutlich weniger reine Vortragszeit zur Verfügung hat.
Vortragsliste:
(Die folgende Liste ist vorläufig)
-
Allgemeine Absolutbeträge auf Körpern (Gouvea, 23-31 [beginnt mit dem Kapitel 2 "Foundations" und endet vor §2.3 Topology] / weiteres
Material auch Robert 77ff)
-
Ultrametrische Topologie und Bewertungsringe (Gouvea, 31-41 [beginnt mit §2.3 Topology und endet vor Kapitel 3] / weiteres
Material auch Robert 37ff)
-
Absolutbeträge auf
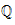 ,
Satz von Ostrowski, Produktformel (Gouvea, 43-49 [beginnt mit Kapitel 3 "p-adic numbers" und endet vor §3.2 Completions] / weiteres Material auch
Robert 85ff)
,
Satz von Ostrowski, Produktformel (Gouvea, 43-49 [beginnt mit Kapitel 3 "p-adic numbers" und endet vor §3.2 Completions] / weiteres Material auch
Robert 85ff)
-
Komplettierung von Körpern, Konstruktion von
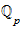 (Gouvea, 49-59 [beginnt mit §3.2 Completions und endet vor §3.3 Exploring
(Gouvea, 49-59 [beginnt mit §3.2 Completions und endet vor §3.3 Exploring 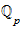 ])
])
-
Grundlegende Eigenschaften von
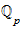 ,
Kompaktheit/Lokalkompaktheit (Gouvea, 59-69 [beginnt mit §3.3 und endet vor §3.4])
,
Kompaktheit/Lokalkompaktheit (Gouvea, 59-69 [beginnt mit §3.3 und endet vor §3.4])
-
Polynome über
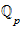 ,
Hensels Lemma (Gouvea, 70-77 [beginnt mit §3.3 und endet vor §3.5 Local and Global] / weiteres Material auch Robert 45ff)
,
Hensels Lemma (Gouvea, 70-77 [beginnt mit §3.3 und endet vor §3.5 Local and Global] / weiteres Material auch Robert 45ff)
-
Erste Ideen zu Global-Lokal Prinzipien,
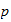 -adische
Fermat-Gleichung (Gouvea, 77-85 [beginnt mit §3.5 und endet vor Kapitel 4])
-adische
Fermat-Gleichung (Gouvea, 77-85 [beginnt mit §3.5 und endet vor Kapitel 4])
-
Grenzwerte, Reihen, Differenzierbarkeit in
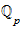 (Gouvea, 87-95 [beginnt mit Kapitel 4 und endet vor §4.3 Power Series])
(Gouvea, 87-95 [beginnt mit Kapitel 4 und endet vor §4.3 Power Series])
-
Potenzreihen in
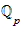 (Gouvea, 95-102 [beginnt mit §4.3 Power Series und endet vor §4.4 Functions defined by power series]
(Gouvea, 95-102 [beginnt mit §4.3 Power Series und endet vor §4.4 Functions defined by power series]
-
Durch Potenzreihen in
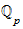 definierte Funktionen, Nullstellen (Strassman's Satz) (Gouvea, 102-111 [beginnt mit §4.4 und endet vor §4.5 Some elementary functions])
definierte Funktionen, Nullstellen (Strassman's Satz) (Gouvea, 102-111 [beginnt mit §4.4 und endet vor §4.5 Some elementary functions])
-
Der
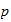 -adische
Logarithmus und die
-adische
Logarithmus und die
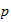 -adische
Exponentialfunktion (Gouvea, 111-123 [beginnt mit §4.5 und endet vor den "binomial series"])
-adische
Exponentialfunktion (Gouvea, 111-123 [beginnt mit §4.5 und endet vor den "binomial series"])
[Kontrastierung mit den komplexen
Versionen]
-
Die
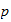 -adische
Interpolation und die
-adische
Interpolation und die
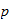 -adische
Gammafunktion (Koblitz, 88-91 +
-adische
Gammafunktion (Koblitz, 88-91 +
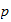 -adische
Interpolation)
-adische
Interpolation)
-
Von p-adischen Zahlen zu projektiven Limiten
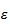 -Umgebung
-Umgebung
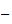 Zahlen sind \nah", wenn ihre Differenz einen kleinen Betrag hat. Man kann
allerdings auch ganze Zahlen \nah" nennen, wenn ihre Differenz durch eine hohe
Potenz einer Primzahl
Zahlen sind \nah", wenn ihre Differenz einen kleinen Betrag hat. Man kann
allerdings auch ganze Zahlen \nah" nennen, wenn ihre Differenz durch eine hohe
Potenz einer Primzahl
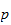 teilbar ist. Ähnlich wie die reellen Zahlen aus den rationalen entstehen,
indem man fordert, dass alle Cauchyfolgen konvergieren sollen, kann man die
rationalen Zahlen auch erweitern, indem man dasselbe für diesen
völlig anderen Begriff von
teilbar ist. Ähnlich wie die reellen Zahlen aus den rationalen entstehen,
indem man fordert, dass alle Cauchyfolgen konvergieren sollen, kann man die
rationalen Zahlen auch erweitern, indem man dasselbe für diesen
völlig anderen Begriff von
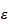 -Umgebung
fordert. Und genau dies sind die berühmten
-Umgebung
fordert. Und genau dies sind die berühmten
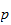 -adischen
Zahlen. Es gibt Folgen, die nicht in den reellen Zahlen konvergieren, aber in
den
-adischen
Zahlen. Es gibt Folgen, die nicht in den reellen Zahlen konvergieren, aber in
den
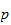 -adischen
-adischen
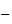 und sogar Folgen, die sowohl
und sogar Folgen, die sowohl
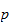 -adisch
wie auch reell konvergieren, aber mit unterschiedlichen Grenzwerten.
-adisch
wie auch reell konvergieren, aber mit unterschiedlichen Grenzwerten.