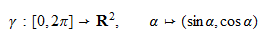 oder aber auch als Nullstellenmenge von
oder aber auch als Nullstellenmenge von
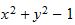 im
im
 definieren. Aber keine dieser Darstellungen ist besonders kanonisch. Allein
schon durch eine andere Wahl von Koordinaten im
definieren. Aber keine dieser Darstellungen ist besonders kanonisch. Allein
schon durch eine andere Wahl von Koordinaten im
 würden wir völlig andere Formeln bekommen. Diese Probleme kann man
auf elegante Weise lösen, indem man einen anderen Blickwinkel einnimmt:
Auf einem geometrischen Gebilde kann man Funktionen betrachten, die (nach
sorgfältiger Begriffsbildung) einen Körper bilden. Entwickelt man
diesen Standpunkt, entpuppt sich schnell, dass es völlig genügt mit
einem abstrakten Körper zu arbeiten, dessen Elemente a priori rein gar
nichts mit Funktionen zu tun haben müssen, und dass "endlich erzeugte
Körper-Erweiterungen von Transzendenzgrad eins" eine erstaunlich
nützliche Definition für (normale algebraische) Kurven ist. In dem
Seminar werden wir die Geometrie von Kurven von diesem Standpunkt entwickeln.
würden wir völlig andere Formeln bekommen. Diese Probleme kann man
auf elegante Weise lösen, indem man einen anderen Blickwinkel einnimmt:
Auf einem geometrischen Gebilde kann man Funktionen betrachten, die (nach
sorgfältiger Begriffsbildung) einen Körper bilden. Entwickelt man
diesen Standpunkt, entpuppt sich schnell, dass es völlig genügt mit
einem abstrakten Körper zu arbeiten, dessen Elemente a priori rein gar
nichts mit Funktionen zu tun haben müssen, und dass "endlich erzeugte
Körper-Erweiterungen von Transzendenzgrad eins" eine erstaunlich
nützliche Definition für (normale algebraische) Kurven ist. In dem
Seminar werden wir die Geometrie von Kurven von diesem Standpunkt entwickeln.Dieses Seminar richtet sich u.a. besonders an Lehramtsstudenten.