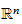Proseminar zu simplizialen Mengen

Termin: Montags, 12:15-14:45 Uhr, SR 404

12 Termine (es entfallen: 1. Mai sowie der Pfingstmontag) Es sind noch Vorträge zu vergeben. Melden Sie sich bei Interesse bitte per E-Mail, oliver.braeunling@math... an der Uni Freiburg

Ablauf:

Alle Vortragenden sollten mindestens eine Woche vor ihrem Vortragstermin zu einer Vorbesprechung kommen, zu der der Vortrag bereits vollständig ausgearbeitet sein soll.
Die Vorträge sollen ca. 80 Minuten lang sein. Man sollte dabei beachten, dass Zwischenfragen der Zuhörer erlaubt und auch erwünscht sind, sodass man effektiv deutlich weniger reine Vortragszeit zur Verfügung hat.

Worum geht es? Einen Graphen kann man sich als aus Punkten und Kanten zusammengesetzte geometrische Struktur vorstellen. Kann man von jedem Punkt des Graphen jeden anderen erreichen? Gibt es geschlossene Wege? Hängen die Antworten auf solche Fragen mit anderen Eigenschaften eines Graphen zusammen?

Statt nur Kanten zu verkleben, kann man auch Dreiecke miteinander verkleben. Schnell gelangt man zu grundlegenden Fragen, z.B. wenn man sich die Oberfläche einer Sphäre als Verklebung lauter kleiner Dreiecke vorstellt, gibt es dann einen Zusammenhang zwischen den Anzahlen der dafür notwendigen Eckpunkte, Kanten und Dreiecke?

Und zerlege ich stattdessen ein anderes Objekt, z.B. einen Torus, in Dreiecke, kann ich aus diesen Kennzahlen der Triangulierung erkennen, ob ich es mit einer Sphäre oder einem Torus zu tun hatte?

Oft werden solche Fragen mit topologischen Räumen behandelt, als Teilmengen des 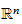$\QTR{Bbb}{R}^{n}$ und man benutzt Hilfsmittel wie Wege, die Fundamentalgruppe, oder gar Analysis.

Wir bestreiten einen anderen Weg, der die Kombinatorik von Triangulierungen, oder allgemeiner simplizialer Zerlegungen in den Mittelpunkt stellt. MATH Für diese Art von Daten gibt es eine mathematische Theorie. Man arbeitet mit simplizialen Komplexen oder simplizialen Mengen. Hierbei handelt es sich um eine kombinatorische Struktur, die in einem relativ präzisen Sinn topologische Strukturen modelliert.

Themen

Graphen, Grundbegriffe
[Diestel, Chapter 1 bis einschließlich §1.3]
- Graphen, Isomorphie
- Untergraphen
- Pfade und Kreise
- Minimale und maximale Länge, Distanz
- Alles immer mit Beispielen verdeutlichen
Euler-Graphen und Hamilton-Kreise
[Diestel, §1.8 (Eulers Rundweg durch Königsberg), Theorem 1.8.1]
Hamilton-Kreise, Kapitel 10 bis einschließlich 10.2.1]
- Eulers klassisches Problem und die Lösung
- Hamilton-Kreise
- Beispiele
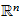
Höhere Dimensionen: Simplizialkomplexe -- abstrakte und geometrische im $\QTR{Bbb}{R}^{n}$
[Pontryagin, Chapter 1, §2, p9-14]
- Erinnerung an Konvexität (Pontryagin wiederholt auch sehr viel lineare Algebra. Das wollen wir entweder völlig weglassen oder sehr stark kürzen)
- Simplizes
- geometrische simpliziale Komplexe
- abstrakte simpliziale Komplexe
- Geometrische Realisierung: das Polyeder 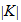eines Komplexes
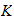
Zusätzliche Informationen finden Sie in [Gallier--Xu, Chapter 3]
Geometrie vs. Kombinatorik: Satz: Abstrakte 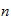-Komplexe lassen sich geometrisch in 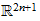realisieren
[Pontryagin, Chapter 1, §2, p14- (beginnt bei [F]), hauptsächlich "Theorem 3"]
- die natürliche Metrik
- Punkte in "allgemeiner Lage"
Flächen: Idee der Normalform und (zulässige) Triangulierungen
[Massey, Chapter 1, §5-6
- Das 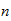-gon, Idee der Normalform
- Triangulierungen (werfen Sie neben Masseys Darstellung auch einen Blick auf [Gallier--Xu, §3.2], die eine unserem Proseminar nähere Sprache verwenden)
- Wie auch Masseys Buch, akzeptieren wir den Satz von Rado zur Existenz einer Triangulierung ohne Beweis
- Viele Beispiele (was ist eine Triangulierung, was keine)
- Beispiele zur Anzahl der 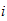-Simplizes in einer Triangulierung
Doppelvortrag: Der Beweis der Klassifikation der Flächen, Teil I
Doppelvortrag: Der Beweis der Klassifikation der Flächen, Teil II
[Massey, Chapter 1, §7]
Diese zwei Vorträge sollten von den Vortragenden gemeinsam vorbereitet werden.
Wir folgend der Darstellung des Beweises im Buch von Massey. Beachten Sie allerdings, dass Gallier--Xu in Chapter 1 eine (auch historische) Übersicht geben. Auch dort findet man viel Material, was diese Vorträge abrunden kann.

Masseys Lemma 7.1 soll in diesem Vortrag nicht vorkommen, wir gliedern es aus:
Satz: Die verbundene Summe von projektiver Ebene und Torus ist homöomorph zur verbundenen Summe von drei projektiven Ebenen
[Massey, Chapter 1, Lemma 7.1]
- im Zentrum des Vortrags soll Lemma 7.1 stehen
- Nach der Diskussion dieses Lemmas widmen wir uns der projektiven Ebene, wie sie mit Selbstüberschneidung im 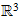$\QTR{Bbb}{R}^{3}$ liegt [Gallier--Xu, Appendix A]
Simpliziale Homologie
[Pontryagin, Chapter 1, §4 "The Betti groups"] Definition simplizialer Homologie
- Beachten Sie auch die ausführliche Darstellung bei [Gallier--Xu, §5.2]
- Beispiele (ähnlich Gallier--Xu).
- Skizzieren Sie auch singuläre Homologie (Gallier--Xu), sprechen Sie dies mit dem nächsten Vortragenden ab, wie Sie das Material aufteilen wollen
Euler Charakteristik und Euler Formel: Anzahl von Simplizes gegebener Dimension vs. Betti-Zahlen
- Der algebraische Blickwinkel auf Homologie:
- Kettenkomplexe, Homologie, Homologie eines Graphen [Weibel, §1.1]
- Morphismen von Kettenkomplexen
- Erläutern Sie genau, inwiefern die simpliziale und (evtl. schon teilweise definierte) singuläre Homologie in dieses abstrakten Baukasten passt
- Veranschaulichen Sie zunächst an reichlichen Beispielen, dass man einen Zusammenhang zwischen den Betti-Zahlen und den Zahlen vermuten kann
- Hauptresultat soll sein: Euler-Charakteristik über Anzahl von Simplizes vs. Homologie [Pontryagin, Chapter 1, §6, Fokus auf "Theorem 9"].
Simpliziale Mengen
[May, §1, und §2 übersichtshaft, Definition: singuläre Homologie aus 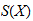für top. Raum. Dies gibt uns einen etwas anderen Blickwinkel auf die singuläre Homologie]
- Definition
- Kan Bedingung
- Konstruktion aus abstrakten simplizialen Komplexen
- geometrische Realisierung (parallel zur geometrischen Realisierung von abstrakten simplizialen Komplexen wie zuvor)
  
  (siehe auch: Lamotke, Kapitel 1, §3, §5)
- Kombinatorische Homotopiegruppen à la Kan (als Mengen)
  [May, §3 -- den Beweis der langen exakten Homotopiesequenz weglassen, Theorem 3.7]
Die kombinatorischen Homotopiegruppen sind Gruppen, und abelsch 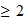$\geq2$ (optional)
[May, §4]