Seminar zur analytischen Zahlentheorie
Di 14-16, SR 404, Eckerstr. 1
Prof. Annette Huber-Klawitter
Dr. Oliver Bräunling
Es sind noch Plätze frei, falls Sie nachträglich einsteigen
möchten!
Thema:
In der analytischen Zahlentheorie behandelt man zahlentheoretische
Fragestellungen mit Methoden aus der Funktionentheorie.
Eine
berühmte Idee in dieser Richtung stammt von Euler: Für
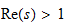 gilt die
Gleichung
gilt die
Gleichung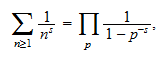 wobei
wobei
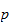 alle Primzahlen durchläuft. Man kann diese Ausdrücke als komplexe
Funktion von
alle Primzahlen durchläuft. Man kann diese Ausdrücke als komplexe
Funktion von
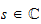 auffassen. Beispielsweise ergibt sich sofort: Gäbe es nur endlich viele
Primzahlen, so wäre
auffassen. Beispielsweise ergibt sich sofort: Gäbe es nur endlich viele
Primzahlen, so wäre
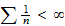 .
Also gibt es unendlich viele Primzahlen. Für diese Aussage gibt es viel
einfachere Beweise, doch Verfeinerungen dieser Methoden erlauben es, sehr
starke Aussagen zu beweisen. Beispielsweise zur Existenz von unendlich vielen
Primzahlen mit zusätzlich vorgegebenen Eigenschaften.
.
Also gibt es unendlich viele Primzahlen. Für diese Aussage gibt es viel
einfachere Beweise, doch Verfeinerungen dieser Methoden erlauben es, sehr
starke Aussagen zu beweisen. Beispielsweise zur Existenz von unendlich vielen
Primzahlen mit zusätzlich vorgegebenen Eigenschaften.
Ablauf:
-
Alle Vortragenden sollten mindestens eine Woche vor
ihrem Vortragstermin zu einer Vorbesprechung kommen, zu der der Vortrag
bereits vollständig ausgearbeitet sein soll.
-
Die Vorträge sollen ca. 80 Minuten lang sein. Man sollte dabei beachten,
dass Zwischenfragen der Zuhörer erlaubt und auch erwünscht sind,
sodass man effektiv deutlich weniger reine Vortragszeit zur Verfügung
hat.
Literatur
-
Serre, J.-P. A Course in Arithmetic, Springer
1996.
-
Lang, S. Introduction to modular forms (GTM
series), Springer, 1987
-
Iwaniec H., Kowalski E. Analytic number theory,
Colloquium Publications, AMS
-
Diamond F., Shurman J. A first course in modular
forms. Graduate Texts in Mathematics, 228. Springer-Verlag, New York, 2005.
-
Apostol, T. Modular functions and Dirichlet
series in number theory, Springer
Wir werden hauptsächlich Serres Buch "A Course in
Arithmetic"folgen.
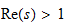 gilt die
Gleichung
gilt die
Gleichung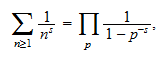 wobei
wobei
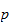 alle Primzahlen durchläuft. Man kann diese Ausdrücke als komplexe
Funktion von
alle Primzahlen durchläuft. Man kann diese Ausdrücke als komplexe
Funktion von
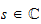 auffassen. Beispielsweise ergibt sich sofort: Gäbe es nur endlich viele
Primzahlen, so wäre
auffassen. Beispielsweise ergibt sich sofort: Gäbe es nur endlich viele
Primzahlen, so wäre
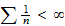 .
Also gibt es unendlich viele Primzahlen. Für diese Aussage gibt es viel
einfachere Beweise, doch Verfeinerungen dieser Methoden erlauben es, sehr
starke Aussagen zu beweisen. Beispielsweise zur Existenz von unendlich vielen
Primzahlen mit zusätzlich vorgegebenen Eigenschaften.
.
Also gibt es unendlich viele Primzahlen. Für diese Aussage gibt es viel
einfachere Beweise, doch Verfeinerungen dieser Methoden erlauben es, sehr
starke Aussagen zu beweisen. Beispielsweise zur Existenz von unendlich vielen
Primzahlen mit zusätzlich vorgegebenen Eigenschaften.