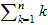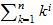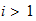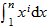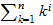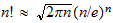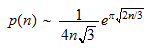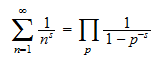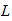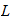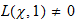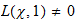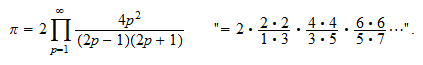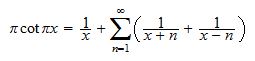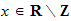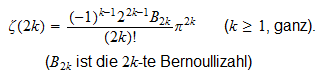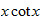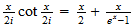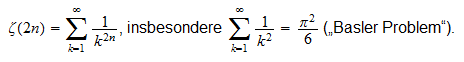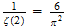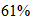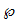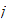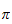Proseminar Zahlentheorie
Mittwochs 12-14, SR 404, Eckerstr. 1
Oliver Bräunling
Vorbesprechung:
SR 414 (Eckerstraße 1), Mittwoch, 8. Juli, 12 Uhr
Anmeldung:
Teilnehmer-Liste bei Frau Frei (Raum 433)
Ablauf:
-
Je nach Teilnehmerzahl sollen die Vorträge einzeln oder zu zweit
vorbereitet und gehalten werden, wobei die Themen gleichmäßig
aufgeteilt werden sollen.
-
Das Programm enthält einige "größere Themen", die zwei
aufeinanderfolgende Vorträge einnehmen. Dies bedeutet, dass sich die
Vortragenden entweder gemeinsam vorbereiten, oder aber zumindest in sehr enger
Abstimmung ihre Themenaufteilung koordinieren.
-
Alle Vortragenden sollten mindestens eine Woche vor ihrem Vortragstermin zu
einer Vorbesprechung kommen, zu der der Vortrag bereits vollständig
ausgearbeitet sein soll.
-
Die Vorträge sollen ca. 80 Minuten lang sein. Man sollte dabei beachten,
dass Zwischenfragen der Zuhörer erlaubt und auch erwünscht sind,
sodass man effektiv deutlich weniger reine Vortragszeit zur Verfügung
hat.
Übersicht zum Thema:
Wie groß ist die Wahrscheinlichkeit, dass zwei zufällig
gewählte natürliche Zahlen teilerfremd sind?
Überraschenderweise
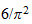 ,
wobei es zunächst völlig unklar erscheinen mag, was Primzahlen
überhaupt mit einer Zahl wie
,
wobei es zunächst völlig unklar erscheinen mag, was Primzahlen
überhaupt mit einer Zahl wie
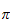 zu tun haben. Wie viele Möglichkeiten gibt es eine natürliche Zahl
zu tun haben. Wie viele Möglichkeiten gibt es eine natürliche Zahl
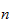 als Summe natürlicher Zahlen zu schreiben? Wenn
als Summe natürlicher Zahlen zu schreiben? Wenn
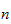 klein ist, kann man das von Hand schnell durchprobieren. Für große
klein ist, kann man das von Hand schnell durchprobieren. Für große
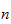 wird dies zunehmend unpraktikabel. Man kann jedoch zeigen, dass je
größer
wird dies zunehmend unpraktikabel. Man kann jedoch zeigen, dass je
größer
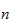 ,
die Zahl
ungefähr
,
die Zahl
ungefähr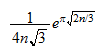 ist. Wir wollen uns mit solchen oder ähnlichen Fragen beschäftigen.
Auch damit, was eine algebraische oder transzendente Zahl ist, und warum es
kein Polynom mit rationalen Koeffizienten gibt, dass bei
ist. Wir wollen uns mit solchen oder ähnlichen Fragen beschäftigen.
Auch damit, was eine algebraische oder transzendente Zahl ist, und warum es
kein Polynom mit rationalen Koeffizienten gibt, dass bei
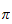 eine Nullstelle hat.
eine Nullstelle hat.
(Sehr vorläufiges) Programm:
-
Erzeugendenfunktionen (D. Newman, Kapitel 1, S. 1-10, endet
vor "An identity of Euler")
Wir schreiben kombinatorische Größen
als Potenzreihen auf und verwenden mit großem Effekt algebraische
Operationen, z.B. die Partialbruchzerlegung, um aus den Eigenschaften dieser
Funktionen etwas über das ursprüngliche kombinatorische Problem zu
sagen.
-
Bernoulli-Zahlen, Polynome und Euler-MacLaurin Summation I
-
(Optional) Bernoulli-Zahlen, Polynome und Euler-MacLaurin Summation
II
Kombiniertes Thema: Die Berechnung von
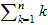 ist Schulstoff. Was ist mit
ist Schulstoff. Was ist mit
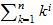 für
für
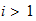 ?
Eine allgemeine Idee ist es, solche Summen durch das
korrespondierende Integral
?
Eine allgemeine Idee ist es, solche Summen durch das
korrespondierende Integral
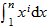 anzunähern; vielleicht kann man den Fehler dieser Annäherung genau
bestimmen? Dies führt auf Bernoulli-Polynome, die Faulhaber'sche Formel
für
anzunähern; vielleicht kann man den Fehler dieser Annäherung genau
bestimmen? Dies führt auf Bernoulli-Polynome, die Faulhaber'sche Formel
für
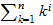 und die Stirling-Formel
und die Stirling-Formel
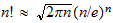 .
Siehe Apostol, §3.3. Evtl. auch Dirichlet's asymptotische Formel
(Apostol, §3.5, Thm. 3.2 + Thm. 3.3).
.
Siehe Apostol, §3.3. Evtl. auch Dirichlet's asymptotische Formel
(Apostol, §3.5, Thm. 3.2 + Thm. 3.3).
-
Wegintegrale und der Integralsatz von Cauchy (z.B.
Jänich)
Wir lernen oder wiederholen, wie man eine komplex
differenzierbare Funktion entlang eines Weges integriert und den zentralen
Integralsatz von Cauchy, der uns noch mehrfach begegnen wird. Das Maximum
Modulus Prinzip.
-
Die Partitionsfunktion I, Asymptotik von Hardy-Ramanujan (D.
Newman, Kapitel 2)
-
Die Partitionsfunktion II, Asymptotik von Hardy-Ramanujan (D.
Newman, Kapitel 2)
Auf wie viele Varianten kann man eine natürliche
Zahl als Summe natürlicher Zahlen
schreiben?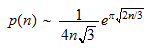 Dies erfordert zwei oder gar drei Vorträge und lässt sich nur
realistisch gemeinsam vorbereiten. Auch die Aufteilung des Materials auf zwei
Vorträge soll von den Vortragenden konzipiert werden.
Dies erfordert zwei oder gar drei Vorträge und lässt sich nur
realistisch gemeinsam vorbereiten. Auch die Aufteilung des Materials auf zwei
Vorträge soll von den Vortragenden konzipiert werden.
-
Die Riemann'sche Zetafunktion, Definition
Dirichlet-Reihen
Wir definieren die Zetafunktion, beweisen die
zentrale
Formel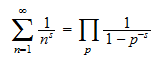 und diskutieren die analytische Fortsetzung, Konvergenz und grundlegende
Eigenschaften von Dirichlet
und diskutieren die analytische Fortsetzung, Konvergenz und grundlegende
Eigenschaften von Dirichlet
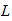 -Reihen
(z.B. Knapp, Kapitel VII, §1 und §2, oder Apostol oder Serre)
-Reihen
(z.B. Knapp, Kapitel VII, §1 und §2, oder Apostol oder Serre)
-
(Optional) Multiplikative Funktionen und
Dirichlet-Reihen
Wir wollen uns mit dem Konzept der
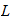 -Reihen
näher beschäftigen.
-Reihen
näher beschäftigen.
-
Dirchlets Satz über Primzahlen in arithmetischen Progressionen
I
-
Dirchlets Satz über Primzahlen in arithmetischen Progressionen
II
Dieser Satz erfordet zwei Vorträge. Eine sinnvolle
Aufteilung wäre: Fourier-Theorie auf endlichen abelschen Gruppen und der
Hauptbeweis ohne die Nichtverschwindungs-Aussage
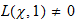 .
Im 2. Vortrag:
.
Im 2. Vortrag:
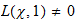 . Bei
Knapp wäre dies Kapitel VII, §3 und §4, ohne Lemma 7.11.
Für die Nichtverschwindung gibt es alternative knappere Argumente als bei
Knapp.
. Bei
Knapp wäre dies Kapitel VII, §3 und §4, ohne Lemma 7.11.
Für die Nichtverschwindung gibt es alternative knappere Argumente als bei
Knapp.
-
Die Gammafunktion und die Formel von Wallis
Wir
diskutieren die Gammafunktion und die Formel von
Wallis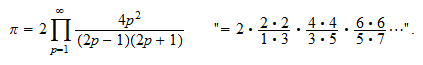 Evtl. Formulierung der Funktionalgleichung der Zetafunktion.
Evtl. Formulierung der Funktionalgleichung der Zetafunktion.
-
Die unendliche Partialbruchdarstellung des
Kotangens
Siehe z.B. Delahaye. Die
Formel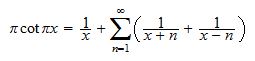 für
für
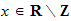 soll gezeigt werden. Als Anwendung dieser Formel zeigt man die berühmte
Formel
soll gezeigt werden. Als Anwendung dieser Formel zeigt man die berühmte
Formel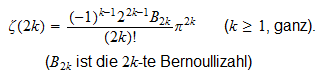 durch Bestimmung der Taylorreihe der Funktion
durch Bestimmung der Taylorreihe der Funktion
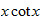 via der Partialbruchdarstellung, sowie Ausnutzung der elementaren
Identität
via der Partialbruchdarstellung, sowie Ausnutzung der elementaren
Identität
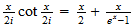 .
Es
folgt
.
Es
folgt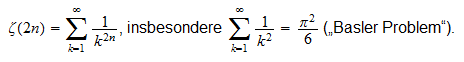 Es gibt auch eine statistische Interpretation: \Die Wahrscheinlichkeit, dass
zwei beliebig gewählte natürliche Zahlen teilerfremd sind, ist genau
Es gibt auch eine statistische Interpretation: \Die Wahrscheinlichkeit, dass
zwei beliebig gewählte natürliche Zahlen teilerfremd sind, ist genau
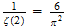 ",
also ca.
",
also ca.
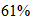 .
.
-
Der Primzahlsatz I
-
Der Primzahlsatz II
aus dem Buch von Newman, oder die
Darstellung von Don Zagier.
-
Algebraische Zahlen und Siegels Lemma
Wir wollen
definieren was eine algebraische Zahl ist und beweisen, dass diese Zahlen
einen Ring formen. Wir wollen einige Grundbegriffe kennenlernen, z.B. die
Norm, und Siegels Lemma über die ganzzahligen Lösungen linearer
Gleichungssysteme kennenleren (S. Lang, Introduction to transcendental
numbers, Chapter 1).
-
Der Sätze von Schneider-Lang und
Gelfond-Schneider.
Wir beweisen den Satz von Schneider-Lang (S.
Lang, Introduction to transcendental numbers, Chapter 3, §1-§3). Der
Satz von Gelfond-Schneider folgt unmittelbar. Die Anwendung auf
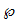 und
und
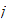 aus dem Buch lassen wir weg.
aus dem Buch lassen wir weg.
-
Abzählbar, überabzählbar
Wir wollen die
Begriffe "abzählbar" und "überabzählbar" kennenlernen. Dann
wollen wir zeigen, dass die reellen und transzendenten Zahlen
überabzählbar sind und die algebraischen abzählbar (Cantor).
Studien/Prüfungsleistung
Literatur:
M. Aigner, G. Ziegler Proofs from THE BOOK (2nd
Edition), Springer, 2000
J. P. Delahaye Pi - Die Story, Birkhäuser,
1999 (Übersetzung des franz. Originals, Le fascinant nombre
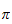 ,
Belin, Pour la Science, 1997)
,
Belin, Pour la Science, 1997)
D. J. Newman Analytic Number Theory, Springer
1998
S. Lang Introduction to transcendental numbers,
Addison-Wesley 1966
T. Apostol Introduction to Analytic Number
Theory, Springer 1976
J.P. Serre A Course in
Arithmetic, Springer
Es gibt zahlreiche weitere Quellen, die vergleichbares
Material abdecken.
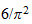 ,
wobei es zunächst völlig unklar erscheinen mag, was Primzahlen
überhaupt mit einer Zahl wie
,
wobei es zunächst völlig unklar erscheinen mag, was Primzahlen
überhaupt mit einer Zahl wie
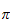 zu tun haben. Wie viele Möglichkeiten gibt es eine natürliche Zahl
zu tun haben. Wie viele Möglichkeiten gibt es eine natürliche Zahl
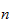 als Summe natürlicher Zahlen zu schreiben? Wenn
als Summe natürlicher Zahlen zu schreiben? Wenn
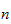 klein ist, kann man das von Hand schnell durchprobieren. Für große
klein ist, kann man das von Hand schnell durchprobieren. Für große
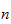 wird dies zunehmend unpraktikabel. Man kann jedoch zeigen, dass je
größer
wird dies zunehmend unpraktikabel. Man kann jedoch zeigen, dass je
größer
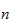 ,
die Zahl
ungefähr
,
die Zahl
ungefähr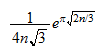 ist. Wir wollen uns mit solchen oder ähnlichen Fragen beschäftigen.
Auch damit, was eine algebraische oder transzendente Zahl ist, und warum es
kein Polynom mit rationalen Koeffizienten gibt, dass bei
ist. Wir wollen uns mit solchen oder ähnlichen Fragen beschäftigen.
Auch damit, was eine algebraische oder transzendente Zahl ist, und warum es
kein Polynom mit rationalen Koeffizienten gibt, dass bei
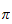 eine Nullstelle hat.
eine Nullstelle hat.