Die Arbeitsgemeinschaft bestand aus fünf Lehramtsstudenten der Mathematik und etwa zehn Schülern des Theodor-Heuss-Gymnasiums Freiburg, vorwiegend aus der elften Klasse. Innerhalb dieser AG wurde den Studenten die Möglichkeit gegeben, erste Stunden selbst vorzubereiten und zu halten, die Vor- und Nachteile des Mathematikunterrichts mit dem Computer kennenzulernen und die Tauglichkeit von Mathematica für den Unterricht zu überprüfen. Die Schüler sollten mit Hilfe von Mathematica an mathematische Probleme herangeführt werden, sie erkennen und mit dem Computer lösen lernen. Als Ausgangspunkt dienten dazu bekannte Aufgabenstellungen aus Klasse 11, wie zum Beispiel Kurvendiskussionen, die dann aber auch durch weitere, den Studenten wesentlich erscheinende Themen vertieft wurden. Als Beispiel dafür seien parametrisierte Kurven genannt, die als Erweiterung von Ortskurven dienten. Ziel war es, vor allem Aufgaben zu behandeln, deren Bearbeitung ohne Computer nicht oder nur mit großem Aufwand möglich gewesen wäre.
Bis auf wenige Ausnahmen hatten weder die Schüler noch die Studenten Vorkenntnisse mit Computeralgebrasystemen, der Umgang mit dem Computer war aber allen vertraut. Die Situation der AG kann natürlich nicht mit dem normalen Unterricht verglichen werden, da hier auf einen "Lehrer" zwei Schüler kamen, aber die grundlegenden Vorzüge und Probleme des Computerunterrichts waren erkennbar.
Die einzelnen Stunden liefen so ab, daß ein oder zwei Studenten die Stunde vorbereiteten und sie, bevor die Schüler dazukamen, 45 Minuten lang mit den übrigen Studenten besprachen. Daran schlossen sich zwei Schulstunden mit den Schülern an, die hauptsächlich von denjenigen Studenten gehalten wurden, die die Stunden vorbereitet hatten. Dabei saßen immer zwei Schüler zusammen an einem Computer. Die übrigen Studenten folgten dem Unterricht, beobachteten das Geschehen oder halfen auch den Schülern bei Problemen, so daß insgesamt eine recht lockere Atmosphäre entstand. Den Schülern wurde eine Betreuung zuteil, von der im Regelunterricht nur geträumt werden darf. Nach dieser Doppelstunde zusammen mit den Schülern kam es zu einer Besprechung der Stunde ohne die Schüler. Dabei wurde die Stunde reflektiert, Gutes und Schlechtes angesprochen und der weitere Verlauf der AG geplant.
Bedingt durch Ferien und Studienfahrten der Schüler, fanden leider insgesamt nur acht Doppelstunden statt, und es gab zum Teil größere Pausen zwischen den einzelnen Sitzungen. Außerdem hatten die meisten Schüler außerhalb der AG keinen Zugang zu Mathematica, so daß es keine Möglichkeit gab, das Gelernte zu vertiefen oder die Syntax der einzelnen Befehle richtig zu lernen. Um dies zu kompensieren, erhielten die Schüler detaillierte Stundenprotokolle.
Mathematica ist ein Vertreter der sogenannten Computeralgebrasysteme. Mit diesen Programmen lassen sich sowohl numerische, als auch symbolische Berechnungen durchführen. Numerisch bedeutet, daß Ergebnisse, die Mathematica ausgibt, durch Näherungsverfahren errechnet und dann gerundet werden. Bei symbolischen Berechnungen liefert Mathematica, soweit das möglich ist, exakte Ergebnisse, zum Beispiel auch Wurzeln und Brüche.
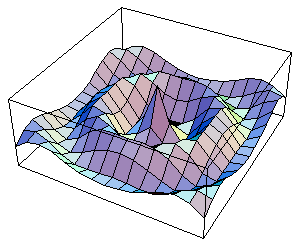
Der Umfang der mathematischen Funktionen von Mathematica ist sehr groß. Er umfaßt Differentiation und Integration, wobei bestimmte und unbestimmte Integrale berechnet werden. Gleichungen, Differentialgleichungen und Gleichungssysteme lassen sich lösen. Mathematica beherrscht Matrizenrechnung und kann mit Vektoren umgehen. Ein wichtiger Aspekt für den Schulunterricht ist die Darstellung von Funktionen in Schaubildern. Dabei lassen sich die Graphen in 2- und 3-dimensionaler Form darstellen; Kontur-, Dichte- und parametrische Plots können ebenfalls erzeugt werden. Eine weitere wichtige Möglichkeit, Mathematica sinnvoll einzusetzen, besteht in der Fähigkeit, Einzelbilder zu einer Animation zusammenzufügen und so mathematische Vorgänge als "Film" darzustellen. Dafür eignen sich zum Beispiel trigonometrische Funktionen, wie man in Abbildung 2 sieht.
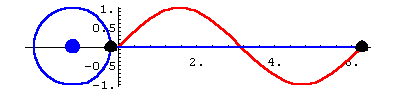
Die Bewegung des Punktes auf dem Kreis und die Erzeugung der Sinuskurve läßt sich in Mathematica als Animation abspielen.
Für den Fall, daß die eingebauten Funktionen nicht ausreichen, stellt Mathematica eine komplexe Programmiersprache zur Verfügung. Damit lassen sich eigene Funktionen definieren, und so die Möglichkeiten von Mathematica auf die eigenen Bedürfnisse anpassen.
Über die mathematischen Fähigkeiten hinaus bietet Mathematica ein fast vollständiges Textverarbeitungssystem, mit dem mathematische Arbeiten dokumentiert werden können. Man kann sogenannte Notebooks erstellen, die neben der Ein- und Ausgabe auch dokumentierenden Text, Überschriften und Anweisungen enthalten können. Mathematica bietet somit auch die Möglichkeit, Arbeitsblätter zu erstellen, die die Schüler dann direkt am Computer bearbeiten können.
Alles in allem ist Mathematica ein sehr komplexes Werkzeug, mit dem sich eine Vielzahl mathematischer Probleme bearbeiten lassen. Innerhalb des Mathematikunterrichts kann man jedoch nur einen kleinen Bruchteil der Möglichkeiten nutzen, und hauptsächlich die sehr gewöhnungsbedürftige Syntax und die Komplexität der Befehle führen immer wieder zu Problemen bei den Schülern.
2. Stunde – Arbeit mit Funktionen
3. Stunde – Arbeit mit Funktionen/Lösen von Gleichungen
4. Stunde – Lösen von Gleichungen
5. Stunde – Lösen von Gleichungssystemen
6. Stunde – Variation freier Parameter
7. Stunde – Ortskurven/Parametrisierte Kurven
8. Stunde – Parametrisierte Kurven
1. Stunde – Variation von Parametern bei einfachen ganzrationalen Funktionen
Thema der Stunde
Die Schüler sollten einen Einblick in die Möglichkeiten von Mathematica erhalten. Das Variieren von Parametern bei einfachen ganzrationalen Funktionen und das Beobachten der Auswirkungen waren weitere Themen der Stunde.
Lernziele
Die Schüler sollten lernen,
Zum Kennenlernen der Möglichkeiten von Mathematica wurde zunächst eine kleine Demonstration des Programms gegeben. Als Beispiele dafür dienten eine dreidimensionale Animation einer Besselfunktion, ein "fliegender Teppich", und eine Kurvendiskussion ganzrationaler Funktionen.
Danach waren die Schüler selbst gefordert. Sie erhielten vorbereitete Notebooks, in denen sie Parameter in Funktionsgleichungen variieren und sich die Bedeutung der einzelnen Parameter mit Hilfe des Plot-Befehls, der das Schaubild einer Funktion zeichnet, klarmachen sollten.
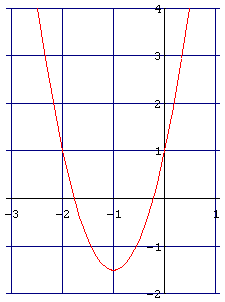
Plot[ a
(x - x0)^2 + y0, {x, -3, 1},
PlotRange
-> {-2,4},
AspectRatio
-> 1.5,
GridLines
-> Automatic,
PlotStyle
-> RGBColor[0,0.5,0]
];
Die Schüler hatten mit den mathematischen Anforderungen dieser Aufgaben keine Probleme, und da die Syntax der benötigten Befehle vorgegeben war, gab es auch mit dem Programm keine Schwierigkeiten. In der ersten Stunde zeigte sich bereits ein großer Vorteil, der sich beim Einsatz von Computern im Mathematikunterricht einstellt: Die Auswirkung der Änderung eines Parameters kann durch einen Knopfdruck sichtbar gemacht werden. Was mit konventionellen Methoden ein langwieriges Neuzeichnen des Schaubildes von Hand nach sich ziehen würde, kann mit Hilfe des Computers innerhalb weniger Sekunden und ohne viel Mühe erledigt werden.
2. Stunde – Arbeit mit Funktionen
Thema der Stunde
Der Schwerpunkt der zweiten Stunde lag auf der Arbeit mit Funktionen.
Lernziele
Die Schüler sollten lernen,
Zu Beginn der Stunde wurden den Schülern an der Tafel und am Computer die Befehle erklärt, die man zum Definieren und Ableiten von Funktionen benötigt. Danach wurde ihnen die Möglichkeit gegeben, damit zu experimentieren. So konnten sie dann Funktionen und deren Ableitungen berechnen und zeichnen lassen.
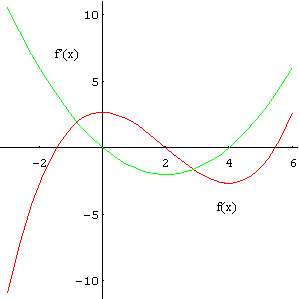
Dann wurde den Schülern erklärt, wie man die Graphen mehrerer Funktionen in ein Schaubild zeichnet. Dabei wurde besonderer Wert auf den Zusammenhang zwischen dem Schaubild einer Funktion und ihrer Ableitung gelegt.
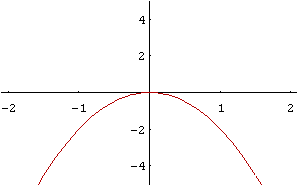
In einem entsprechenden Schaubild, siehe Abbildung 3, läßt sich leicht erkennen, daß bei einer Extremstelle der Funktion der Graph der Ableitung einen Nulldurchgang besitzt. Bei einer Wendestelle der Funktion hat die Ableitung ein Extremum. Mit Hilfe des Computers ließen sich dabei auch noch leicht weitere Ableitungen einbauen und deren Merkmale betrachten.
Im Anschluß wurde den Schülern die Möglichkeit gegeben, mit dem Gelernten, vor allem mit dem Plot-Befehl und der Ableitung von Funktionen, zu experimentieren. Dabei entwickelten die Schüler einen Ehrgeiz, möglichst wilde Funktionen zu zeichnen, die sie von Hand nie hätten darstellen können – die Funktion sin(1/x) war noch eine der harmloseren Art.
Beobachtung
Die Frage nach den mathematischen Hintergründen war dabei für die Schüler unwichtig (und wohl eher lästig). Aber zu Beginn der AG konnte man wohl auch noch nicht mehr erwarten. Hier stand noch die Bedienung von Mathematica im Vordergrund.
Im Gegensatz zur ersten Sitzung wurden in dieser Stunde keine fertigen Notebooks vorgegeben, in denen die Schüler nur Änderungen vornehmen mußten, sondern jeder einzelne Befehl mußte selbst eingegeben werden. Dabei zeigte sich, daß die Syntax von Mathematica sehr komplex und für den Anfänger sehr verwirrend ist. Selbst der kleinste Fehler, eine vergessene Klammer oder ein Komma zuwenig, kann eine Reihe von Fehlermeldungen zur Folge haben. Es mußte daher sehr viel Zeit aufgewendet werden, Fehler in der Syntax zu verbessern, so daß für die eigentliche Arbeit, Mathematik mit dem Computer zu betreiben, nur noch wenig Zeit übrigblieb.
3. Stunde – Arbeit mit Funktionen/Lösen von Gleichungen
Thema der Stunde
Im ersten Teil der Stunde wurde die Arbeit mit Funktionen noch einmal aufgegriffen. Die weitere Stunde wurde dann benutzt, um ein neues Thema zu beginnen: das Lösen von Gleichungen.
Lernziele
Die Schüler sollten lernen,
Ablauf der Stunde
Die benötigten Befehle für die Definition zusammengesetzter Funktionen wurden an der Tafel und am Computer erklärt, danach erhielten die Schüler ein ausgedrucktes Arbeitsblatt, auf dem Aufgaben zu diesem Themen vorbereitet waren. Diese sollten sie dann selbständig lösen.
(a) f(x) = x^3 für x<1
3*x-2 für x>1
(b) f(x) = -x für x<0
x für x>0
(c) f(x) = (x+2)^2 für x<-1
x^2 für -1<x<1
(x-2)^2 für 1<x
(d) f(x) = -1/x für -2<x<-1
x für -1<x<1
1/x für 1<x<2
{{x -> -Sqrt[2]}, {x -> Sqrt[2]}}
NSolve[x^2-2 == 0, x]
{{x -> -1.41421}, {x -> 1.41421}}
.............2
...........-b
- Sqrt[b - 4 a c]
{{x ->
---------------------},
....................2
a
.........2
.......-b
+ Sqrt[b - 4 a c]
{x ->
---------------------}}
..............2
a
Danach wurden zu diesem Thema Aufgaben bearbeitet, die vom Lösen einfacher Gleichungen bis zur grafischen Bestimmung von Nullstellen und Extremstellen reichten, und auch das bisher Gelernte, das Ableiten von Funktionen und das Zeichnen von Schaubildern, vertieften.
f5a[x_]
= x^3 - 3 x^2 + x + 1/2;
f5b[x_]
= Sqrt[9 - x^2];
f5c[x_]
= 1/4 x^4 - x^3 + x^2;
f5d[x_]
= 1/4 x^4 - 1/3 x^3 - x^2;
f5e[x_]
= x^6 - 2 x^3 + 1;
Beim Lösen von Gleichungen zeigte sich ein generelles Problem, das beim Arbeiten mit dem Computer häufig zu beobachten ist: Die Schüler akzeptieren die Ergebnisse, die der Computer liefert, ohne darüber nachzudenken – "was der Computer ausrechnet, wird schon stimmen."
{{x ->
-0.743745}, {x -> 1.20521 - 0.583275 I},
{x ->
1.20521 + 0.583275 I}}
4. Stunde – Lösen von Gleichungen
Thema der Stunde
Der Schwerpunkt dieser Stunde lag wiederum auf der Lösung von Gleichungen.
Lernziele
Die Schüler sollten lernen,
Ablauf der Stunde
Mit dem Gelernten der ersten drei Stunden waren die Schüler nun fast soweit, eine Kurvendiskussion durchzuführen, da diese zu einem großen Teil aus dem Lösen von Gleichungen besteht. In dieser Stunde sollten sie das restliche Rüstzeug dafür erhalten. Die Schüler erhielten dazu eine Aufgabe, die sie zunächst selbständig lösen sollten und durch die sie an das gewünschte Problem herangeführt werden sollten.
f(x) = 1/4 x^3 - 1/2 x^2 - 2x + 1
a) die Nullstellen.
b) die Extremstellen.
c) die Wendestellen.
d) Zeichne die Schaubilder der Funktion und der ersten
beiden Ableitungen in ein Koordinatensystem.
Beobachtungen
In den Stunden zuvor war uns schon aufgefallen, daß die Schüler nicht viel von der Dokumentation der Ergebnisse hielten. Bei den Kurvendiskussionen wurde das besonders deutlich, da dabei viele Werte berechnet werden und dadurch leicht Unklarheiten auftreten. Die Schüler berechneten zwar brav die gewünschten Ergebnisse. Bei der Überprüfung der Ergebnisse war aber alles so unübersichtlich, daß man Probleme hatte, bestimmte Werte zu finden. Daher wollten wir die Schüler anleiten, zu ihren Ergebnissen auch einen Kommentar zu schreiben und damit das Ganze etwas übersichtlicher zu gestalten. Dieses Vorhaben stieß jedoch auf wenig Gegenliebe.
Darin zeigt sich wieder einmal, daß die Schüler die gewünschten Aufgaben zwar ausführen, aber nur wenig über die Hintergründe nachdenken. Es findet kaum Reflexion statt, die Ergebnisse werden als "gottgegeben" hingenommen. Sicher spielen dabei auch die Probleme bei der Beherrschung von Mathematica eine Rolle.
Deshalb ist es wichtig, daß der Lehrer
Die Schüler sollen nicht nur mechanisch vorgegebene Methoden annehmen und diese wiederkäuen. Sie sollen zu "mündigen Bürgern im mathematischen Staat" erzogen werden, über ihr Tun nachdenken.
5. Stunde – Lösen von Gleichungssystemen
Thema der Stunde
Nachdem in den letzten Stunden das Lösen von einzelnen Gleichungen im Vordergrund stand, sollten in dieser Stunde Gleichungssysteme gelöst werden.
Lernziele
Die Schüler sollten lernen,
Verlauf der Stunde
Die Schüler wurden durch die Aufgabe, eine Funktion durch vorgegebene Punkte zu bestimmen, auf das Thema "Lineare Gleichungssysteme" hingeführt. Dies sollte selbständig bearbeitet werden.
Als Erweiterung dieser Aufgabenstellung wurden auch noch Tangentenbestimmungen an vorgegebenen Funktionsgraphen bearbeitet.
{c -> -2, m -> -4}
Beobachtung
Als unbestreitbarer Vorteil bei der Bestimmung von Funktionen durch gegebene Punkte oder bei Tangentenbestimmungen erwies sich im Gegensatz zur konventionellen Methode "zu Fuß" wiederum einmal die Möglichkeit, die Ergebnisse zu visualisieren. Mit dem Computer kann man sich den Graphen der Funktion und die Tangente leicht aufzeichnen lassen und so die Ergebnisse anhand der Zeichnung überprüfen.
In dieser Stunde fiel uns noch ein Problem auf, was aber nicht direkt mit dem Computerunterricht zusammenhängt – Schüler neigen dazu, Formeln auswendig zu lernen und sie bei Bedarf dann herunterzubeten.
Daher ist es Aufgabe des Lehrers,
6. Stunde – Variation freier Parameter
Thema der Stunde
In dieser Stunde wurde ein Bezug zur ersten Stunde hergestellt. Es ging um die Variation von freien Parametern in Funktionsgleichungen und deren Bedeutung.
Lernziele
Die Schüler sollten lernen,
Ablauf der Stunde
Im Gegensatz zur ersten Stunde wurde dieses Mal ein anderes Hilfsmittel verwendet, um die Bedeutung der freien Parameter zu verdeutlichen. Nicht mit dem einfachen Plot-Befehl wurde gearbeitet, die Schüler sollten sich anhand von Animationen die Auswirkungen der Änderungen klarmachen.
Zuerst wurde die Motivation für eine solche Animation gegeben: Bei einfachen Funktionen, zum Beispiel Parabeln mit der Funktionsgleichung f(x)=ax² läßt sich noch im Kopf überblicken, was geschieht, wenn man den Parameter ändert. Was aber geht bei komplizierteren Funktionen vor sich?
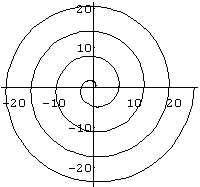
Der Do-Befehl, mit dem man Animationen erstellt, wurde dann an einem einfachen Beispiel, anhand einer Parabel, eingeführt (siehe Abbildung 5). Danach wurden verschiedene Aufgaben von den Schülern selbständig bearbeitet, bei denen immer auch Fragen zu beantworten waren, damit den Schülern die Bedeutung der Parameter verdeutlicht wurde.
g3(x) = x^2 + p*x + 1 ; [-3;3]
Durch welchen Punkt verlaufen alle Parabeln?
Wie verändert sich die Anzahl der Nullstellen mit
p?
Für welche p besitzt die Parabel genau einen Schnittpunkt
mit der x-Achse?
Den Schülern hat es unheimlichen Spaß gemacht, mit den Animationen zu arbeiten. Es war etwas völlig Neues für sie, die Bedeutung der freien Parameter in bewegten Bildern zu sehen. Der Lehrer muß allerdings darauf achten, daß für die Schüler der Spaß am Herumspielen mit diesen Animationen nicht zu sehr im Vordergrund steht und die mathematischen Zusammenhänge darüber nicht vergessen werden.
7. Stunde – Ortskurven/ Parametrisierte Kurven
Thema der Stunde
Aus aktuellem Anlaß, die Schüler hatten gerade eine Klassenarbeit geschrieben, stiegen wir in dieser Stunde mit der Bestimmung von Ortskurven ein. Dieses Thema bot dann an, das Thema parametrisierte Kurven zu vertiefen.
Lernziele
Die Schüler sollten lernen,
Ablauf der Stunde
Da alle Befehle und mathematischen Grundlagen zur Bestimmung von Ortskurven vorhanden waren, wurde mit einer Aufgabe begonnen, die von den Schülern selbständig bearbeitet wurde. Mit dieser Aufgabe wurde auch die Animation aus der letzten Stunde wiederholt.
g4[x_]:=x^2+q x-q;
Durch welchen Punkt gehen alle Parabeln?
Was für eine Kurve beschreiben die Scheitelpunkte?
Für welches q wird der maximale Scheitelpunkt angenommen?
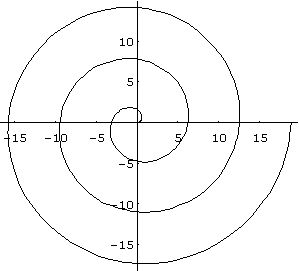
Danach wurde eine andere Möglichkeit vorgestellt, Kurven darzustellen: Kurven in parametrisierter Form – ein Thema, das den Schülern völlig neu war und auch einige Probleme mit sich brachte.
Anstatt den Parameter q zu eliminieren und eine Funktion in Abhängigkeit von x und y zu erhalten, ist es möglich, die x- und y-Werte des Scheitels in Abhängigkeit vom Parameter q aufzutragen. Mathematica stellt dazu einen eigenen Befehl zur Verfügung: ParametricPlot. Die parametrisierten Kurven wurden dann vertieft und den Schülern der Unterschied zu "normalen" Funktionen klargemacht. Bei den parametrisierten Kurven lassen sich auch Schaubilder zeichnen, die sich mit dem normalen Plot-Befehl nicht darstellen lassen, da es keine Funktionen im üblichen Sinne sind (siehe Abbildung 5).
Beobachtungen
Die Erklärung dieser für die Schüler neuen Art, Kurven darzustellen, nahm sehr viel Zeit in Anspruch, so daß für die Bearbeitung von Aufgaben zu diesem Thema keine Zeit mehr blieb.
Den Schülern schien es Spaß zu machen, etwas Neues zu lernen und sie wollten mehr über die parametrisierten Kurven erfahren. Daher entschlossen wir uns, in der letzten Stunde dieses Thema noch einmal aufzugreifen.
8. Stunde – Parametrisierte Kurven
Thema der Stunde
Da die Schüler in der Stunde zuvor von den parametrisierten Kurven sehr angetan waren, wurde dieses Thema noch einmal vertieft. Außerdem fand ein Gespräch mit den Schülern über den Verlauf der AG statt.
Lernziele
Die Schüler sollten lernen,
Ablauf der Stunde
In dieser letzten Stunde der Arbeitsgemeinschaft sollten die Schüler die Möglichkeit erhalten, auch ein bißchen mit Mathematica zu spielen. Da die Schüler an der parametrisierten Darstellung von Kurven sehr interessiert waren, bot sich dieses Thema dazu an. Den Schülern wurde noch einmal ausführlich der Hintergrund dieser Kurven erklärt, zum Beispiel anhand einer Animation eines Kreises. Danach erhielten sie ein Arbeitsblatt mit verschiedenen Aufgaben zum Thema parametrisierte Kurven, das sie im Laufe der Stunde bearbeiten sollten. Diese Aufgaben boten auch viel Gelegenheit, selbst Dinge auszuprobieren.
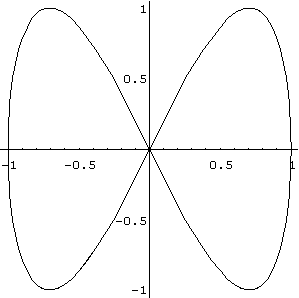
Im Anschluß an die Bearbeitung dieser Aufgaben folgte ein Gespräch mit den Schülern über die Arbeitsgemeinschaft: Wurden ihre Erwartungen erfüllt? Was hätte man besser machen können? Was hat ihnen die AG gebracht?
Außerdem wurde den Schülern ein Fragebogen ausgeteilt, in dem sie ihre Erfahrungen noch einmal schriftlich wiedergeben sollten. Leider wurden von den etwa 10 Fragebögen nur 4 ausgefüllt zurückgegeben, so daß eine sinnvolle ausführliche Auswertung nicht möglich ist. (Der Fragebogen ist als Anhang C abgedruckt.)
Beobachtungen
In dieser Stunde hat sich wieder einmal gezeigt, daß es den Schülern am meisten Spaß macht, selbst Dinge am Computer auszuprobieren und sich verwegene Kurven aufzeichnen zu lassen. Der mathematische Hintergrund ist dabei nur Nebensache. Da dies aber die letzte Stunde war, sollte den Schülern auch etwas geboten werden, was ihnen Spaß macht. Deshalb wurde dieser Effekt mit in Kauf genommen.
Da eine sinnvolle Auswertung der Fragebögen nicht in Frage kommt, soll hier einmal eine Tendenz dargestellt werden:
4. Fachdidaktische Überlegungen
Zur Arbeitsgemeinschaft
Zunächst sollte noch einmal gesagt werden, daß diese Arbeitsgemeinschaft nicht unbedingt mit dem Regelunterricht verglichen werden kann. Im Gegensatz zum normalen Unterricht mit bis zu 30 Schülern waren hier meistens weniger als zehn Schüler anwesend, die in Zweiergruppen an den Computern saßen. Anstatt 15 waren also nur fünf Gruppen zu betreuen. Außerdem waren immer 5 Studenten anwesend, so daß das Verhältnis von "Lehrern" und Schülern unglaublich gut und auch eine Individualbetreuung möglich war. Da es eine freiwillige AG war, waren die Schüler auch sehr motiviert und arbeiteten gut mit.
Als Nachteil erwies sich die relativ geringe Stundenzahl und die geringe Verfügbarkeit des Programms. Mit nur acht Doppelstunden und vielen Unterbrechungen durch Ferien und Studienfahrt mußte viel wiederholt werden. Da die Schüler nur zu Zeiten der AG, also einmal pro Woche 90 Minuten, Zugang zu dem Programm hatten, konnten sie das Gelernte zu Hause nicht vertiefen. Es ergaben sich immer wieder Probleme mit der Syntax der Befehle.
Mathematica und andere Computeralgebrasysteme im Unterricht
Mathematica selbst erwies sich als nur bedingt für den Unterricht geeignet. Seine komplizierte Syntax ist für die Schüler schwer zu erlernen. Die Komplexität der Befehle und die Vielfalt der Möglichkeiten waren ein großes Hindernis beim sinnvollen Umgang mit dem Programm.
Auf diesem Gebiet muß an der Software noch viel gearbeitet werden, damit ein vernünftiges Arbeiten mit dem Computer ermöglicht wird. Ein Computeralgebrasystem, das in Zukunft im Unterricht eingesetzt werden soll, sollte folgende Voraussetzungen erfüllen:
Ein großer Vorteil eines Computeralgebrasystems sind unbestreitbar seine grafischen Eigenschaften. Wo bisher mühsam Wertetabellen erstellt und die Kurven von Hand gezeichnet werden mußten, kann mit dem Computer schnell das gewünschte Schaubild erstellt werden. Der Schüler sieht sofort, was eine Änderung in der Funktionsgleichung im Schaubild der Funktion bewirkt. Auch durch die Animationen können mathematische Inhalte, zum Beispiel die trigonometrischen Funktionen oder auch die Ableitung, sehr schön illustriert werden.
Grundsätzliche Überlegungen zum Computerunterricht
Die Anforderungen an die Lehrer beim Computerunterricht sind hoch. Die Einarbeitung in das Computeralgebrasystem und die Unterrichtsvorbereitung erfordern sehr viel Zeit. Da die Schüler hauptsächlich eigenverantwortlich arbeiten, müssen Arbeitsblätter oder Notebooks erstellt werden, die die Arbeitsanweisungen für die Schüler enthalten. Auch der Unterricht selbst ist sehr anstrengend. Der Lehrer muß blitzschnell umschalten und sich in die verschiedenen Schülerarbeiten einfinden können. Er muß auf fachliche Fragen antworten, individuelle Hilfen bei der Systembedienung und bei der Umsetzung der Lösungsideen geben.
Ein weiteres großes Problem stellte sich im Laufe der AG heraus: Wie gewinne ich als Lehrer die Aufmerksamkeit der Schüler? Dazu ist es sinnvoll, genau gegliederte Abschnitte festzulegen:
Im Laufe dieser Arbeitsgemeinschaft haben wir verschiedene Arbeits- und Unterrichtsformen mit dem Computer ausprobiert.
Am besten geeignet ist wohl zu Beginn das Konzept mit den fertigen Notebooks, da dies am schnellsten Erfolgserlebnisse verspricht. Wenn die Schüler dann im Laufe des Unterrichts mehr Übung mit dem Programm und dessen Syntax haben, kann man von den vorgegebenen Befehlen abgehen und den Schülern immer mehr Freiheit lassen. Jede dieser Arbeitsformen sollte jedoch mit dem Anschreiben der Befehle an die Tafel kombiniert werden. Dadurch können sich die Schüler bei kleinen Unsicherheiten mit dem Blick an die Tafel selbst schnell helfen. Dabei sollte noch genügend Zeit bleiben, neben den programmtechnischen Details auch mathematische Inhalte zu vermitteln.
Fazit
Computer sind für den Unterricht eine große Bereicherung, wenn es um das Visualisieren von Ergebnissen und Graphen geht. Darin liegt die große Stärke des Computers. Um vernünftig mit den Schülern daran arbeiten zu können, ist aber eine lange Einarbeitung der Schüler und auch des Lehrers in das verwendete Programm notwendig. Das kostet viel Zeit – Zeit, die meistens nicht vorhanden ist.
Ein weiterer Aspekt beim Arbeiten mit dem Computer ist die Ausstattung der Schulen mit ausreichend vielen Geräten. Um mit einer Klasse sinnvoll mit dem Computer arbeiten zu können, muß es jederzeit möglich sein, den Computer zu benutzen. Das ist aber heute noch nicht der Fall. Nur die wenigsten Schulen sind mit einer ausreichenden Anzahl von Geräten versorgt.
Auf längere Sicht wird der Computer den Mathematikunterricht ganz bestimmt verändern. Auf welche Weise er das tun wird, kann heute jedoch noch nicht mit Bestimmtheit vorausgesagt werden.
Anhang A: Die Aufgaben aus der Arbeitsgemeinschaft im Überblick
2. und 3. Stunde – Arbeit mit Funktionen/Lösen von Gleichungen
4. Stunde – Lösen von Gleichungen
5. Stunde – Lösen von Gleichungssystemen
6. Stunde – Variation freier Parameter
7. Stunde – Ortskurven/Parametrisierte Kurven
8. Stunde – Parametrisierte Kurven
1. Stunde – Variation von Parametern bei einfachen ganzrationalen Funktionen
P1 (0|1.5), P2 (3|0), P3 (-1|-2), P4 (0.5|2).
Verändere die Parameter a, x0, y0 so, daß
a) der Scheitel der Parabel im Punkt P1 liegt.
b) der Scheitel der Parabel im Punkt P2 liegt.
c) der Scheitel der Parabel im Punkt P3 liegt.
d) der Scheitel der Parabel im Ursprung bleibt, und die
Parabel durch den Punkt P4 geht.
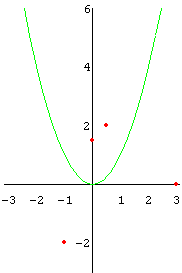
Ändere die Parameter der Funktionsgleichung im "Plot"-Befehl.
Plot [
a (x - x0)^2 + y0, {x, -3, 1},
PlotRange->{-2,4},
AspectRatio
->1.5,
GridLines
->Automatic,
PlotStyle->
RGBColor[0,0,.7]
];
Spiegle das Schaubild von f an der x-Achse, d.h. wähle a, x0 und y0 so, daß das Schaubild der so erhaltenen Funktion g das Spiegelbild von f bezüglich der x-Achse ist.
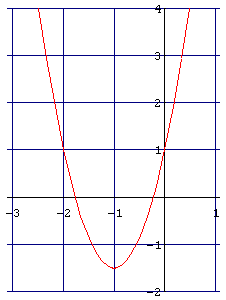
(* Hier kannst du die Parameter der Funktionsgleichung ändern *)
a = 2;
x0 = 0;
y0 = 2;
g [x_]
= a (x-x0)^2 + y0;
f [x_]
= 2 x^2 +2;
(* Befehle zum Zeichnen der Schaubilder: *)
Plot [{f[x],
g[x]}, {x, -4,4},
PlotRange->
{-6,6},
AspectRatio->6/4,
PlotStyle->{RGBColor
[1,0,0]}
];
Spiegle das Schaubild von f an der y-Achse, d.h. wähle a, x0 und y0 so, daß das Schaubild der so erhaltenen Funktion g das Spiegelbild von f bezüglich der y-Achse ist.
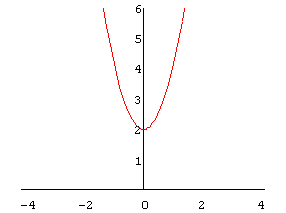
a = 1/2;
x0 = 1;
y0 = -1;
g [x_]
= a (x-x0)^2 + y0;
f [x_]
= 1/2 (x-1)^2 -1;
(* Befehle zum Zeichnen der Schaubilder: *)
UP = Plot
[f[x], {x, -6,6},
PlotRange->
{-2,6},AspectRatio->8/12,
PlotStyle->{RGBColor
[1,0,0]},
DisplayFunction->Identity
];
NP = Plot
[g[x], {x, -6,6},
PlotRange->
{-2,6},AspectRatio->8/12,
PlotStyle->{RGBColor
[0,0.5,0]}, DisplayFunction->Identity
];
Show[UP,
NP,
DisplayFunction->$DisplayFunction
];
Spiegle das Schaubild von f am Ursprung, d.h. wähle a, x0 und y0 so, daß das Schaubild der so erhaltenen Funktion g das Spiegelbild von f bezüglich des Ursprungs ist.
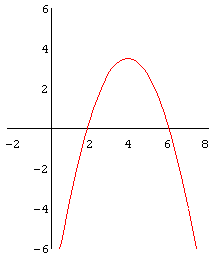
(* Hier kannst du die Parameter der Funktionsgleichung ändern *)
a = -3/4;
x0 = 4;
y0 = 3.5;
g [x_]
= a (x-x0)^2 + y0;
f [x_]
= -3/4 (x-4)^2 + 3.5;
(* Befehle zum Zeichnen der Schaubilder: *)
UP = Plot
[f[x], {x, -8,8},
PlotRange->
{-6,6},AspectRatio->12/16,
PlotStyle->{RGBColor
[1,0,0]},
DisplayFunction->Identity
];
NP = Plot
[g[x], {x, -8,8},
PlotRange->
{-6,6},AspectRatio->12/16,
PlotStyle->{RGBColor
[0,0.5,0]},
DisplayFunction->Identity
];
Show[UP,
NP,
DisplayFunction->$DisplayFunction
];
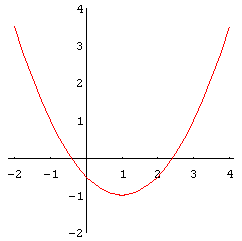
Spiegle das Schaubild von f am Punkt P ( 1|-1 ), d.h. wähle a, x0 und y0 so, daß das Schaubild der so erhaltenen Funktion g das Spiegelbild von f bezüglich des Punktes P ist.
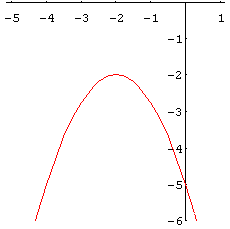
(* Hier kannst du die Parameter der Funktionsgleichung ändern *)
a = -3/4;
x0 = -2;
y0 = -2;
g [x_]
= a (x-x0)^2 + y0;
f [x_]
= -3/4 (x+2)^2 - 2;
(* Befehle zum Zeichnen der Schaubilder: *)
UP = Plot
[f[x], {x, -6,8},
PlotRange->
{-8,6},AspectRatio->1,
PlotStyle->{RGBColor
[1,0,0]},
DisplayFunction->Identity
];
NP = Plot
[g[x], {x, -6,8},
PlotRange->
{-8,6},AspectRatio->1,
PlotStyle->{RGBColor
[0,0.5,0]},
DisplayFunction->Identity
];
PP = ListPlot[{{1,-1}},
PlotStyle->{RGBColor[1,0,0],
PointSize[0.05]},
DisplayFunction->Identity
];
Show[UP,
NP, PP,
DisplayFunction->$DisplayFunction
];
a) Verändere die Parameter a, b, c und d und beobachte
dabei, wie sich das Schaubild der Funktion verändert.
b) Verändere die Parameter so, daß der Wendepunkt
der ursprünglichen Funktion im Ursprung liegt.
c) Verändere die Parameter so, daß das Schaubild
von f keine Extrempunkte mehr hat.
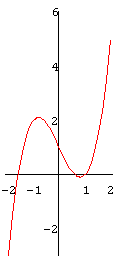
(* Hier kannst du die Parameter der Funktionsgleichung verändern *)
a = 1;
b = 0;
c = -2;
d = 1;
g[x_]
= a x^3 + b x^2 + c x + d;
f [x_]
= x^3 - 2 x + 1;
(* Befehle zum Zeichnen der Schaubilder: *)
Plot [{f[x],g[x]},
{x, -5,5},
PlotRange->
{-4,6},AspectRatio->1,
PlotStyle->{RGBColor
[1,0,0]}
];
Laß Dir irgendwelche Funktionen zeichnen, die Du schon immer einmal sehen wolltest. Nutze dazu den "Plot"-Befehl aus den vorherigen Aufgaben.
Vorsicht: Achte genau auf die Schreibweise!
(* Hier kannst Du Deine Befehle eingeben *)
2. und 3. Stunde – Arbeit mit Funktionen/Lösen von Gleichungen
(a) f(x) = x^3 für x<1
3*x-2 für x>1
(b) f(x) = -x für x<0
x für x>0
(c) f(x) = (x+2)^2 für x<-1
x^2 für -1<x<1
(x-2)^2 für 1<x
(d) f(x) = -1/x für -2<x<-1
x für -1<x<1
1/x für 1<x<2
(e) Gauß-Klammer [x] : liefert die größte,
ganze Zahl unterhalb von x
f(x) = Floor[x]
Der Befehl "Floor[x]" in Mathematica entspricht
der Gauß-Klammer.
(f) Bestimme die Funktionsgleichung des folgenden Graphen:
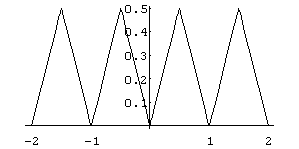
Hinweis : Verwende den Befehl Floor[ ]
(a) 3*x -7 = 0 nach x
(b) x^2 - x - 2 = 0 nach x
(c) m*x + b = 0 nach m und x
(d) 2*x^2 + b*x = -2 nach b und x
(e) 231*x^3 + 82*x^2 - 469*x -68 = 0 nach x
(f) x^3 + a*x^2 + b*x + c = 0 nach a, b, c und x
(b1) x^2 + x - 4 = 0
(b2) x^5 - 3154/15015*x^4 - 6014/15015*x^3 - 20/3003*x^2
+ 157/5005*x + 19/5005 == 0;
(a) f(x) = x^2 + 2*x - 3
(b) f(x) = x^3 + 7/3*x^2 + 1/4*x - 3/2
(c) f(x) = x^2 + 1
(d) f(x) = 1/16*x^3 - x + 2
(e) f(x) = 1/3*x^3 - x^2 - ½
(f) Verschiebe den Graphen der Funktion aus (e) so, daß
:
(f1) der Graph mit der x-Achse vier Punkte gemeinsam
hat.
(f2) der Graph keine Punkte mit der x-Achse gemeinsam
hat.
(g) f(x) = 1/50*x^5 - 1/10*x^4
Beispiel :
f[x_] =
2*x^2 - 3*x + 1;
Plot[{f[x],f'[x],f''[x]},{x,-1,2},
ApectRatio
-> 1.2,
PlotStyle
-> {RGBColor[1,0,0], RBColor[0,0,1], RGBColor[0,1,0]}
];
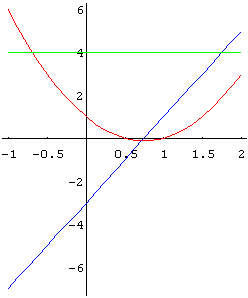
Solve[f[x]==0,x]
1
{{x ->
-}, {x -> 1}}
2
Solve[f'[x]==0,x]
3
{{x ->
-}}
4
(a) f(x) = x^3 - 3 x^2 + x + 1/2
(b) f(x) = Sqrt[9 - x^2]
(c) f(x) = 1/4 x^4 - x^3 + x^2
(d) f(x) = 1/4 x^4 - 1/3 x^3 - x^2
(e) f(x) = x^6 - 2 x^3 + 1
f(x) = 1/4 x^3 - 1/2 x^2 - 2x + 1
a) die Nullstellen.
b) die Extremstellen.
c) die Wendestellen.
d) Zeichne die Funktion und die ersten beiden Ableitungen
in ein Schaubild.
a) die Extremstellen
b) die Wendestelle
und gib die Extrem- bzw. Wendepunkte in einer Tabelle aus.
i) f(x) = x^4 - 4x^2 +1
ii) f(x) = 3x^5 - 5x^4
iii) f(x) = 3x^4 - 8x^3 + 6x^2
iv) f(x) = 1/4x^4 -1/2x^3+x
v) f(x) = Sqrt[x] - 1/4x^2
untersuche sie auf Nullstellen, Extrema und Wendepunkte und gib das Ergebnis benutzererfreundlich aus.
5. Stunde – Lösen von Gleichungssystemen
Erstelle zu jeder der angegebenen linearen Funktion eine Reihe von Schaubildern, indem Du den jeweils freien Parameter von -3 bis +3 mit einer Schrittweite von 0.5 laufen läßt.
a) f1(x) = m*x - 1 im Intervall [-2;2]
b) f2(x) = a*x + a + 1 im Intervall [-4;4]
Welcher Punkt liegt auf allen Kurven von f1 bzw. f2?
Verändere den freien Parameter wie in Aufgabe 1, d. h. von -3 bis +3 mit einer Schrittweite von 0.5. (falls nichts anderes angegeben!). Verwende die angegebenen Intervalle.
a) g1(x) = (x - b)^2 - 1 ; [-3;3]
Was bewirkt b im Schaubild?
Auf welcher Kurve läuft der Scheitelpunkt der Parabeln?
Wie verändern sich die Nullstellen?
b) g2(x) = 1/2*(x - 1)^2 + c ; [-2;4]
Was bewirkt c im Schaubild?
Was ist allen Scheitelpunkten gemeinsam?
Für welchen Wert von c geht die Parabel durch den
Ursprung?
c) g3(x) = x^2 + p*x + 1 ; [-3;3]
Durch welchen Punkt verlaufen alle Parabeln?
Wie verändert sich die Anzahl der Nullstellen mit
p?
Für welche p besitzt die Parabel genau einen Punkt
mit der x-Achse?
d) g4(x) = x^2 + q*x - q ; [-2;4] q von -6 bis 2 ,Schritt
0.5
Durch welchen Punkt gehen alle Parabeln?
Was für eine Kurve beschreiben die Scheitelpunkte?
Für welches p wird der maximale Scheitelpunkt angenommen
?
Parameter : von -2 bis 2 mit Schrittweite 0.25. Intervalle sind angegeben.
a) h1(x) = x^3 + c*x ; [-2;2]
Wie hängt die Anzahl der Nullstellen von c ab?
Zeichne zusätzlich in jedes Schaubild die lineare
Funktion c*x.
b) h2(x) = x^3 + b*x^2 ; [-3;3]
Wie verhalten sich die Nullstellen bzw. die Extremwerte?
Auf welcher Kurve verläuft der von (0;0) verschiedene
Extremwert?
c) h3(x) = a*x^3 - 3*x + 2 ; [-3;3]
Wie verhalten sich die Nullstellen?
Wie verhält sich die Steigung im Schnittpunkt mit
der y-Achse?
Für welche a hat der Graph genau zwei Nullstellen?
g[x_] := x^2 + q x - q;
a) Zeichne die Funktionen für die verschiedenen Werte
von q.
Mache eine Animation.
b) Durch welchen Punkt gehen alle Parabeln ?
c) Was für eine Kurve beschreiben die Scheitelpunkte
?
Für welches q wird der maximale Scheitelpunkt angenommen
?
h[x_] := x^3 + b x^2;
a) Zeichne die Funktionen für die verschiedenen Werte
von b.
Mache eine Animation.
b) Beschreibe, wie sich die Nullstellen bzw. die Extremwerte
in Abhängigkeit vom Parameter b verhalten?
Auf welcher Kurve bewegt sich der von (0;0) verschiedene
Extrempunkt ?
ft[x_] = 1/(6t) x^3 - x^2 + 3/2t x;
a) Zeichne die Schaubilder Kt der Funktion für t
von 0.5 bis 4 in Schritten von 0.5 .
b) Untersuche Kt auf Hoch-, Tief- und Wendepunkte. Notiere
die Punkte.
c) Bestimme die Gleichung der Ortskurve aller Wendepunkte
Wt von Kt.
d) Bestimme die Gleichung der Wendetangente für
allgemeines t.
Für welches t > 0 geht die Wendetangente durch den
Punkt P(4/3 | 0)?
e) Für welches t > 0 ist die Normale durch den Wendepunkt
senkrecht zur 2. Winkelhalbierenden?
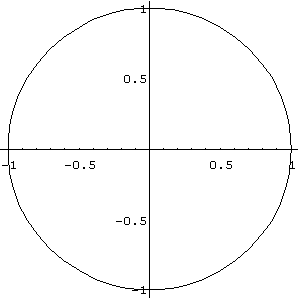
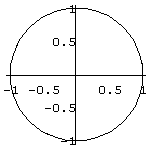
Der Kreis soll variiert werden. Dazu verallgemeinern wir die Gleichung des Kreises mit Hilfe von Parametern:
x = a +
Cos[t];
y = b
+ Sin[t];
a) Überlege, was sich ändert, wenn man einsetzt:
a=1; b=0;
a=0; b=1;
a=2; b=-1;
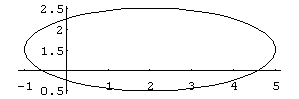
b) Versuche nun, folgende Figur zu erzeugen:
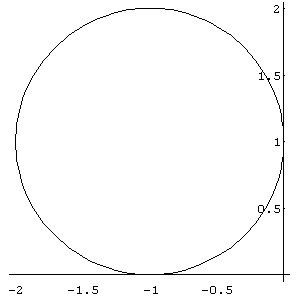
c) Nun ändern wir die Gleichung folgendermaßen ab:
Clear[a,b,x,y,t];
x = a
Cos[t];
y = b
Sin[t];
Variiere selbst die Parameter a und b und beschreibe, was sich ändert.
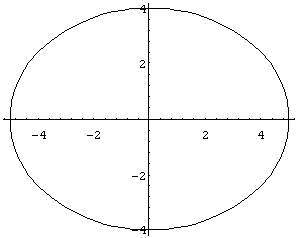
e) Zuletzt betrachten wir folgende Variation:
Clear[a,b,x,y];
x = Cos[a
t];
y = Sin[b
t];
Verändere wieder die Parameter a und b und beschreibe, was passiert.

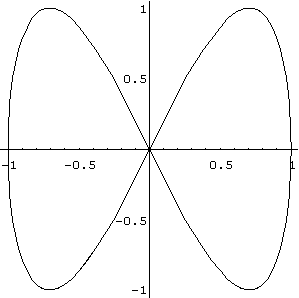
Anhang B: Übersicht über die in der AG verwendeten Mathematica-Befehle
Zusatzbefehle: PlotStyle
Grafikbefehl, mit dem z.B. die Kurvenfarbe geändert wird
AspectRatio
ermöglicht es, die Achsen passend zu skalieren
GridLines
ermöglicht das Einzeichnen von Gitterlinien
PlotRange
legt den Wertebereich fest
Beispiel:
1
Power::infy:
Infinite expression -- encountered.
0.
Plot::plnr: CompiledFunction[{x}, <<1>>, -CompiledCode-][x] is not a machine-size real number at x = 0..
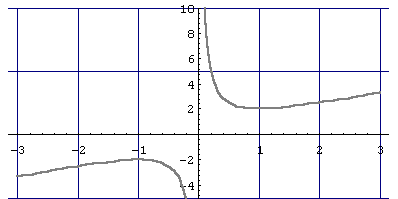
Bemerkung :
Die Fehlermeldung gibt auf einen Hinweis darauf, daß die Funktion bei x = 0 nicht definiert ist. Die Zeichnung wird aber trotzdem erstellt.
Syntax: Plot[{f1,f2,f3}, {x, xmin, xmax}]f''[x]
berechnet die zweite Ableitung,
f'''[x]
die dritte usw.
Beispiel:
7
{{x ->
-}}
3
Beispiel:
{{x -> 2.33333}}
Zusatzbefehle: TableHeadings
Bestimmt die Beschriftung der Zeilen und Spalten
Syntax: Solve[{Gleichung1, Gleichung2,...,GleichungN, {x1,x2,...,xN}]
Beispiel:
5 1
{{x ->
-, y -> -}}
2 2
Beispiel:
{{x -> 2.5, y -> 0.5}}
Beispiel:
{2, 3, 5, 7, 11, 13}
Part[Primzahlen, 4]
7
Beispiel:
Beim Zeichnen von mehreren Schaubildern mit dem "Do"-Befehl, muß darauf geachtet werden, die Option "PlotRange" anzugeben, da Mathematica sonst nicht bei allen Schaubildern dieselben Wertebereiche verwendet.
Syntax: ParametricPlot[{x(t),y(t)}, {t, tmin, tmax}]Zusatzbefehle: (dieselben wie beim "Plot"-Befehl)
Beispiel:
Anhang C: Fragebogen zur Arbeitsgemeinschaft
Mathematisches Institut D-79104 Freiburg
der Universität Freiburg Eckerstr.1
Abteilung für Elementarmathematik Tel.:
0761/203-5617
und Didaktik der Mathematik Fax.: 0761/203-5621
Liebe Schüler,
um eine Rückmeldung über die AG zu erhalten, würden wir Euch bitten, diesen Fragebogen auszufüllen und ihn am nächsten Montag (07. Juli) mitzubringen. Wir hoffen, Euch hat die AG genauso viel Spaß gemacht wie uns.
Wenn ja, wozu benutzt Du ihn?
r Textverarbeitung r Programmieren r Grafik/Sound r Datenverwaltung
r Internet r Spiele r Sonstiges, nämlich_________________
Wenn ja, mit welchem? __________________________________________________
Wenn ja, in welchem Fach, bei welchen Themen, welche Programme? _____________
_____________________________________________________________________
_____________________________________________________________________
r Sonstiges ___________________________________________________________
_____________________________________________________________________
r nicht sinnvoll, weil ____________________________________________________
_____________________________________________________________________
r Teilweise sinnvoll, z.B. bei _____________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
Anhang D: Literatur zum Thema Computer im Unterricht
Dieter Brandt, Mathematisches Institut
28.8.98