Johannes Schornstein
3% exakt - oder irgendwo zwischen 2,4 und 3,6%??
Von der Genauigkeit offizieller Zahlen
1. Beispiel
Eben höre ich im Radio, dass unser Finanzminister wieder einmal bekräftigt, dass die BRD die Maastricht-Bedingungen einhalten werde und die Gesamtverschuldung nur maximal 3,0% des Bruttoinlandsprodukts betragen würde. "Und drei Komma Null sind drei Komma null und nicht drei Komma eins oder drei Komma zwei!" stellt er klar. Denn andere hatten vorgeschlagen, auch 3,2% Prozent Verschuldung noch zu akzeptieren. Der Streit ist voll entbrannt. Man spricht von der "punktgenauen" Einhaltung der Verträge. Mir fällt ein, was dazu bei Morgenstern (1973, S.259) steht: "Es ist deprimierend zu sehen, dass sogar ... führende Fachleute ... die Zahlen für das Bruttosozialprodukt .. in ihrem Nominalwert ernst nehmen. Offensichtlich wurde ... noch niemals nach der Genauigkeit dieser Zahlen gefragt ..."
Dabei liegen entsprechend Ergebnisse vor. 1971 bekam Kuznets für Untersuchungen über Fehlerbereiche in Volkseinkommensstatistiken den Nobelpreis. Er konnte Wirtschaftszweige nach der Größe der Fehler ihrer Statistik in drei Gruppen einteilen. Für die Schätzung(!) des Volkseinkommens kam er dann zu einem daraus resultierenden Fehler von ±20%, den er auf Grund der zusätzlichen Annahme der gegenseitigen Kompensation auf ±10% reduzieren konnte. (s. auch Laussermayer 1996)
Theo Waigels Drei-Komma-Null kann also auch eine 3,3 sein - falls das offizielle BIP 10% zu hoch ist, oder eine 2,7 sein - falls es 10% zu klein ist. Und falls man bei den Schulden auch einen Fehler von 10% für möglich hält, schwankt die exakte 3,0 irgendwo zwischen 2,4 und 3,6.
2. Genaue Zahlen sind glaubhaft.
In einem Fortbildungslehrgang, den ich leitete, gab ein Referent - Dr. der Mathematik und Professor am Studienseminar - die Verdunstungsraten in der BRD mit 54% und in der DDR mit 75% an. Als wir uns ob der Genauigkeit und des Unterschieds sehr wunderten, sprach er voll Hochachtung: "Da gibt es die Vereinigung Deutscher Gewässerschutz, die haben ganz genaue Untersuchungen und solch sehr genauen Zahlen." Wie ungenau sie wirklich sind, darüber unten mehr. Aber die genaue Zahl täuschte eine genaue Untersuchung vor.
In meiner Steuererklärung gebe ich immer die Zinsen in der Form "Konto 3309282 Zins: 987,65 DM" an und fassen zusammen: "kleiner Konten Zins: unter 50,00 DM". Ob es auch genau 987,65 DM sind, wurde ich noch nie gefragt, wohl aber, ob die 50,00 DM auch wirklich nicht überschritten sind.
Als ich die Zahl der an meinem Buch interessierten Studenten mit 34 gegenüber dem Verlag angab, sagte meine Frau: "Da hast Du aber genau gezählt." Tatsache war, dass der Verlag dies von mir verlangt hatte, ich jedoch die Zahl grob geschätzt und bewusst keine glatte Zahl gewählt hatte, um Exaktheit vorzutäuschen. Wie man sieht, mit Erfolg, denn der Verlag schickte 34 Bücher.
In einer Arbeitsgruppe von Mathematikern des OSA Freiburg äußerte ich Zweifel an der Anzahl von 272 Eiern, die jeder Bundesbürger 1983 durchschnittlich gegessen haben soll. Ein Kollege wies jede Zweifel zurück: "Wenn es nur ein Eier mehr oder weniger gewesen wäre, dann hätte man sich ja um - äh - ja, 60 Millionen verzählen müssen. Das ist nicht möglich!"
Die Untersuchung muß so genau sein, daß die Zahl stimmt.
Der Innenminister vergleicht die Krankheitstage im öffentlichen Dienst mit denen von Betriebskrankenkassen (BKK) und Krankenkassen der gesetzlichen Krankenversicherung (GKV). Bei den Bundesbediensteten liegt danach die Krankheitsrate pro Arbeitnehmer (insgesamt 550 000) und Jahr bei 16,8 Tagen (Arbeiter 23, Angestellte 16, Beamte 12), bei BKK und GKV aber bei 13,3 Tagen. Angesichts dieses großen Unterschieds scheint es klar, dass er einen Maßnahmenkatalog beschließt. Und hier wird der Glaube an die genaue Zahl gefährlich.
Wer allerdings sich nicht nur auf die Zeitungen verlässt, die natürlich mit einer gewissen Häme über die Untersuchung berichten, der findet im "Das Bundesministerium des Inneren informiert" vom 10.1.97 den Satz: "Die Statistiken folgen einer unterschiedlichen Methodik und wurden deshalb vergleichbar gemacht." Die Ergebnisse von BKK und GKV mussten z.B. "umgerechnet auf Krankheitstage" werden. Und beim Bund wurden nur 50% der "Kurzzeiterkrankungen (1-3 Tage)" eingerechnet. 50% , das ist so ungenau, das kann nicht stimmen, dachte ich mir und erhielt auf Nachfragen vom Bundesministerium des Inneren folgende Antworten: "Bei GKV und BKK werden die Kurzzeiterkrankungen nur teilweise erfasst; soweit mir bekannt(!), liegt der Erfassungsgrad unter 50 v. H." (Damit ist eins klar: Man wählte 50%, damit die Krankheitstage im öffentlichen Dienst auf keinen Fall zu gering ausfielen.) Ich habe auch nach der Genauigkeit der vorgelegten Zahlen gefragt. Antwort: "Ich gehe von einer sehr großen Genauigkeit der Erhebung (des BMdI, J.S.) aus... Über die Genauigkeit der von BKK und GKV erhobenen Daten liegen mir keine Angaben vor. Mir ist nicht bekannt, ob das Bundesministerium für Gesundheit über entsprechende Angaben verfügt."
O. Morgenstern hat recht: Nach der Genauigkeit der vorliegenden Zahlen fragt keiner. Ich möchte nicht behaupten, dass die vorgelegten Zahlen falsch sind. Aber es ist unredlich, eigene Zahl mit andern, deren Fehlerschranke man nicht kennt, zu vergleichen.
P.S.: Am 20.9. finde ich in der Zeitung, dass man beim BGS statt wie vorgegeben die Krankheitstag die Kalendertage gezählt hat!! Also waren die BMdI Zahlen hier zu hoch - und bei Zoll auch.
3. Überprüfung der Zahlen
Meist ist es unmöglich, irgendwelche Zahlen zu überprüfen.
Wird z.B. ein Wahlergebnis angegeben, natürlich auf eine Stimme genau, dann ist diese Präzision gegen jeden Zweifel erhaben, ja, wer Zweifel erhebt, gilt als Verleumder. Eine Nachzählung bloß zur Kontrolle (oder für meinen Artikel) kann es nicht geben.
Ich bin allerdings auf einen Fall gestoßen, bei dem eine Nachzählung erfolgte, die OB-Wahl in Neu-Ulm. Ich glaube, dass die dort aufgetretenen Zählfehler auch sonst überall dort auftreten, wo Menschen am Werk sind. Ich selbst habe es erlebt, dass ich samt der übrigen Wahlkommision ein Wahlergebnis mit 100%iger Sicherheit falsch festgesetzt hätte, hätte nicht einer die Frage gestellt: "Was sind das da eigentlich für Wahlzettel?" Trotz Querrechnen und Überprüfen hatten wir schlicht einen Stapel übersehen!
Ich hätte gerne überprüft, wie das BMdI die BKK- und GKV-Daten in Krankheitstage umgerechnet hat, wie genau diese Daten sind usw. Aber das wäre dann wohl eine volkswirtschaftliche Doktorarbeit geworden. Auch in andern Fällen uferten die Untersuchungen aus. So muss sich der Leser mit dem begnügen, was ich herausgefunden hat, und ggf. eine eigene Recherche anstellen. (Für Hinweise bin ich dankbar.)
Oft war ich auf die Information anderer angewiesen (ein für einen reinen Mathematiker seltsames Gefühl). Manche, die ich angesprochen habe, wie etwa der Leiter des statistischen Amt der Stadt Freiburg, Herr Dr. von Hamm, gaben mir bereitwillig Antwort. Ihnen hier nochmals herzlichen Dank. Andere mauerte etwas. Wenige antworteten gar nicht. Allen gemeinsam ist, dass keiner eine präzise Angabe der Fehlerschranke seiner präzisen Zahlen geben wollte bzw. konnte. Herr von Hamm lehnte jede Schätzung ab, da ihm entsprechende Daten fehlen. Andere erwiesen auf die Güte ihrer Daten, wollten sich aber nicht auf eine Fehlerschranke festlegen. (Ich hatte ±1%, 5%, 10% vorgeschlagen.) Statt dessen erhielt ich verbale Beschreibungen wie "Diese Daten sind im allgemeinen recht genau."
Manchmal allerdings tun einem die offizielle Zahlen den Gefallen und widersprechen sich selbst. Hier kommentarlos einige Beispiele:
a) Nach dem "Statistischen Jahrbuch 1991 für das Ausland" wurden 1990 weltweit Güter und Dienstleistungen im Werte von 2 912 Milliarden US-Dollar importiert, aber nur solche im Werte von 2 824 Milliarden US-Dollar exportiert.
b) Nach einer Studien aus Großbritannien haben englische Frauen "auf das Leben verteilt" im Durchschnitt 2,9 verschieden Sexualpartner, englischen Männer dagegen 11 (siehe Krämer (1991)). Die Badische Zeitung berichtete im Juni 97, dass in Schweden diese Zahl bei den Frauen bei 5 und bei den Männern bei 7 liege.
c) Nach jeder Volkszählung gibt es mehr verheiratete Frauen als verheiratete Männer (und es gibt auffallend viele Frauen im Alter zwischen 18 und 25.)
d) Die Vorratsänderung (Netto-Lagerzu- und -abgänge) für 1985 wurden 1986 mit +14,2 Milliarden angegeben, dann in den Folgejahren mit +7,5 Milliarden, -1,4 Milliarden und -0,7 Milliarden.
4. Wie kommen diese Zahlen zustande?
4.1 Sie werden - selten - durch Zählen ermittelt.
Die 272 Eier, die wir 1983 aßen, wurden nicht durch Zählung ermittelt (s.u.). Hier irrte der Kollege (s.o.). Wie ist es aber, wenn man wirklich zählt?
Am 21.5.1996 musste die Stichwahl entscheiden, ob Beate Merk (CSU) oder Gerhard Hölzel (SPD) Oberbürgermeister der 50 000-Einwohner-Stadt Neu-Ulm werde würde. Die Aufgabe, die Stimmen auszuzählen, erscheint einfach gegenüber der Zählung von rund 20 Milliarden Eiern oder den Einwohnern von Freiburg, wo z.B. dauernd jemand geboren wird. Das offizielle Endergebnis der Stichwahl lautet deshalb auch:
Von den 34 658 Wahlberechtigten von Neu-Ulm haben an der Stichwahl 19 049 gewählt, dabei entfielen auf Frau Merk 9 463 und auf Herrn Hötzel 9 460 Stimmen.
Ein übliches, wenn auch knappes Ergebnis.
Daraus ersieht man allerdings nicht, wie es zustande kam. Am Wahlabend hatte Frau Merk noch 44 Stimmen Vorsprung. Weil man Unregelmäßigkeiten vermutete, wurde die Wahl sofort angefochten und das Landratsamt aufgefordert, eine Nachzählung zu veranlassen. Nach langem Zögern fand diese am 19.6.96 statt. Dabei ergaben sich folgende Verschiebungen in den insgesamt 66 Stimmbezirken:
a) Durch falsche Zuordnung:
Stimmbezirk: 07 24 33 44 50 Saldo
Merk +2 - 6 - 1 - 19 +1 - 23
Hötzel - 2 +6 +1 +19 - 1 +23
b) Stimmbezirk 61: Es wurde ein ungültiger Stimmzettel im Hötzel-Stapel gefunden.
Wichtig erscheint mir, dass hier in rund 10% aller Wahllokale das Ergebnis korrigiert werden musste. Nun glaube ich nicht, dass im 44. Wahllokal 19 Hötzel-Stimmzettel auf dem Merk-Stapel lagen. Üblich ist es, zehn Stimmzettel zu bündeln. Ich vermute, dass zwei solcher Bündel auf den Merk-Stapel geraten sind und zum Ausgleich ein Merk-Stimmzettel auf dem Hötzel-Stapel.
Es fällt auf, dass es mal 2, mal 6, mal 19 falsche Zuordnungen gab, aber nie zwei, die sich aufhoben. Ich vermute weiter, dass dies zwar vorgekommen ist, man aber - verständlicherweise - solche Fehler nicht veröffentlichte. Ich habe auch auf Nachfragen nichts weiteres dazu erfahren. Mit andern Worten: Ich vermute einen höheren Anteil der Wahllokale mit Fehlern als 10%.
Nun hatte Herr Hötzel eine Stimme Vorsprung! Jetzt nun kommt ein weiterer Gesichtspunkt hinzu: Bei den oben dokumentierten Zählfehlern gehe ich von ganz normalem menschlichen Irrtum aus. Nun aber ordnete Landrat Schick (CSU) eine erneute Zählung an, obwohl die gerade erfolgte Auszählung von zwei Mitarbeitern des Landratsamtes getrennt überprüft war - bei Abweichung sogar mehrfach. Was ihm natürlich den Vorwurf der Manipulation einbrachte. Denn die Nachzählung am nächsten Tag - die Stimmzettel waren zeitweise unbewacht - ergab im Stimmbezirk 13 eine Merk-Stimme im Hötzel-Stapel, im Stimmbezirk 47 tauchte plötzlich einen Stimmzettel im Hötzel-Stapel mit einem Doppelkreuz (Warum wurde eine derart auffälliger Stimmzettel bei den mehrmaligen vorangehenden Zählungen nicht entdeckt?) auf, also eine ungültige Stimme, sowie eine mit dem Zusatz "nur für Hötzel", die für ungültig erklärt wurde. Damit hatte die CSU-Kandidatin drei Stimmen Vorsprung, es steht 9463 zu 9460 und Herr Schick (CSU) verzichtete auf weitere Überprüfungen.
Und damit kommen wir zu einer weiteren Frage: Wann ist eine Stimme eine Stimme? Nach einem Bericht der Badischen Zeitung hätte der "nur für Hötzel"-Stimmzettel nicht für ungültig erklärt werden dürfen.
An diesem Beispiel ersehen wir drei klassische Fehlerquelle. Erstens kommt es auch bei der gewissenhaftesten Messung zu Zähl- oder Messfehlern. Dann kann es durchaus im Interesse der Beteiligten liegen, eine Zahl hoch oder tief zu rechnen. Und drittens stellt sich immer die Frage der Bewertung oder Festlegung (s. auch Abschnitt 6.)
4.2 Sie werden - meist - nicht gemessen, sondern berechnet.
4.2.1 Berechnung durch Addition
In einer Broschüre der Vereinigung Deutscher Gewässerschutz (1995) wird das Wasservorkommen der Erde durch Addition ermittelt:
Wasser der Weltmeere: 1 321 900 000 km³
Polareis: 29 180 000 km³
Grundwasser: 8 595 000 km³
Oberflächenwasser: 230 000 km³
Wolken: 13 000 km³
Wasser der Erde 1 359 918 000 km³
Obwohl man das "Wasser der Weltmeere" nur auf hunderttausend Kubikkilometer genau angegeben hat - die Nullen am Ende sind nicht ernst gemeint und dienen nur der Festlegung der Größenordnung - wird das Endergebnis auf tausend Kubikkilometer genau angegeben.
So kann ich auch mein Vermögen auf den Pfennig genau angeben: Mein Haus - rund 500 000 DM, minus Schulden von ... plus Sparkonten ... plus ... minus ... plus dem Inhalt meiner Geldbörse von 52,34 DM ...
Was machen wir daraus in der Schule? Im Band "Wasser und Mathematik" der Beiträge zur Lehrerfortbildung des Studienseminars (Gymnasien) Rottweil werden diese Zahlen ernst genommen und z.B. ermittelt, dass 97,22% unseres Wassers Meerwasser ist. Glaubt irgendeiner wirklich, dass man den Meerwasseranteil auf ein Zehntel Promill genau bestimmen kann? Der Untertitel dieses Bandes heißt "Kann die Mathematik dazu beitragen, die Einstellung von Jugendlichen zu Problemen der Gesellschaft und der Umwelt positiv zu beeinflussen?" Es wird eine Hinwendung zu realitätsorientierten Problemen fordert und ausdrücklich gefolgert: "Die Präzision ... , die so oft die Seele der reinen Mathematik ausmacht, bleibt meist unerreicht." Aber hier wird den Schüler doch diese nicht vorhandene Präzision vorgegaukelt. Wäre es nicht auch Aufgabe dieses Band gewesen, die Zahlen in vernünftiger Genauigkeit aufzuarbeiten, damit sie die Lehrer der siebten Klasse, für die diese Unterrrichtseinheit gedacht ist, im Unterricht in vernünftiger Weise verwenden?
4.2.2 Berechnung durch Multiplikation/Division
Die USA-Post gab 1983 die Maße ihrer Adlerkopfmarke mit 48,768 mm x 43,434 mm an, also auf Tausendstel Millimeter. Schon durch die Luftfeuchtigkeit schwankt aber die Länge um mehr ein Tausendstel Millimeter! Diese Genauigkeit resultiert aus der Umrechnung der Originalmaße von 1,92 Zoll x 1,71 Zoll in mm ( 1 Zoll = 25,4 mm).
Bei der Verdunstungsrate von 54% in der alten BRD (s.o.) ermittelt die Vereinigung Deutscher Gewässerschutz die Niederschlagsmenge durch Multiplikation der Fläche von rund 250 000 km² (nach Lexikon 248 601 km²) der BRD mit der "Niederschlagshöhe" von 837 mm. Dabei sind die 837 mm ein langjähriger Durchschnitt, wobei langjährig oft 30 Jahre bedeutet. (Genaues kann ich nicht sagen, da sich der Herr, der für die Vereinigung Deutscher Gewässerschutz die Berechnungen machte, in vornehmes Schweigen hüllte, als ich ihn mehrfach anschrieb.) Es werden ausdrücklich Trockenjahre (1959) mit nur 74% (!) dieser Niederschlagsmenge ebenso erwähnt wie die Schwankungen in einzelnen Bundesländern (Niedersachen 1959: 58%). Dieser Wert schwankt also durchaus um einige Prozent, je nach dem ob man zufällig einige Trockenjahr mehr oder weniger erwischt hat.
Der Wert 837 mm · 250 000 km² wird großzügig auf 200 Milliarden m³ (statt 208 Milliarden m³) gerundet. Nun berechnet man durch Addition die Verdunstung:
Pflanzen 81 Milliarden m³
Boden 25 Milliarden m³
Seen/Flüsse 2,6 Milliarden m³
108,6 Milliarden m³
Es wird später ausdrücklich erwähnt, dass in trockenen und heißen Sommern die Verdunstungsrate höher liegt. Obwohl man obigen Zahlen deutlich ansieht, dass es nur grobe Schätzwerte sind, wird jetzt nur minimal auf 108 Milliarden m³ gerundet, dann aber exakt gerechnet: 108:200 = 0,54, also ist die Verdunstungsrate 54%! Hätte man z.B. die Niederschlagsmenge mit 208 Milliarden m³ statt mit 200 Milliarden m³ angenommen, wäre man auf 52% gekommen. Trotz dieser offensichtlichen Ungereimtheiten flößt diese genaue Zahl dem Professor höchsten Respekt ein!
In einem Bericht der Bundesregierung (1993) heißt es: "Nach den Schätzungen der UNESCO würden ... (in der BRD, J.S.) zwischen 468 667 und 1 874 666 ... Personen zu den Analphabeten gehören." Die UNESCO hatte nämlich 1990 die Analphabetenrate der BRD auf 0,75% bis 3% geschätzt. Obwohl im Bericht zunächst ausdrücklich festgestellt wird, dass es "zur genauen Anzahl der Analphabeten keine gesicherten Angaben" gibt, wurde diese grobe Schätzung exakt umgerechnet: Die Prozentzahlen wurden mit der offiziellen Einwohnerzahl (über 15 Jahren) von 62 488 880 multipliziert (Ergebnis: 468 666,6 bzw. 1 874 666,4) und auf 468 667 bzw. 1 874 666 exakt gerundet!
Die Zahl der Eier, die wir essen, werden "aus nationalen Versorgungsbilanzen berechnet, also nicht durch repräsentative Erhebungen", wie mir in einem Brief des Bundesministeriums für Ernährung, Landwirtschaft und Forsten mitgeteilt wurde. Dazu werden "Erzeugung, Lagerbestandsänderungen und Außenhandel saldiert... . Durch Division des Verbrauchs durch die Bevölkerungszahl ergibt sich der Je-Kopf-Verbrauch. Dieser Verbrauch entspricht allerdings nicht dem menschlichen Verzehr (Marktverluste, Zubereitungs- und Schälverluste, Abschnitte, Verderb usw. sind nicht quantifizierbar). ... Die Qualität der in diese Berechnung eingehenden Daten ist im allgemeinen sehr hoch. Ein neues Erhebungsverfahren ... hat jedoch ... seit Januar 1993 zu einem merklichen methodischen Bruch geführt und gewisse Einschränkungen bei den Ergebnissen erforderlich gemacht."
Merke: Weil sich die Erhebungsmethode geändert hat, hast Du heute ein Ei mehr oder weniger gegessen.
5. Wie genau sind die Zahlen wirklich?
Am 31.12.95 hatte Freiburg offiziell 199 273 Einwohner, am 1.1.96 aber 185 294. Beim Jahreswechsel wurde nicht etwa ein Ortsteil aus Freiburg ausgegliedert, wie man vielleicht vermuten könnte, die unterschiedlichen Einwohnerzahlen wurden nur von zwei unterschiedlichen Institutionen ermittelt, nämlich vom Statistischen Landesamt Baden-Württemberg (erste Zahl) und vom Amt für Statistik und Einwohnerwesen der Stadt Freiburg. Die Differenz beträgt rund 7%.
Eine Ursache liegt nach Meinung beider Institutionen darin, dass manche in Freiburg registrierte Abmeldungen nicht nach Stuttgart gelangt. Dem Landesamt wird zur Vermeidung von Doppelmeldungen nur die Anmeldung am neuen Wohnort mitgeteilt. Daraus ergibt sich dann - zumindest theoretisch - die entsprechende Abmeldung am bisherigen Hauptwohnort.
Wahrscheinlich gibt es aber auch den folgenden Fall: Ein Student hat entsprechend unserem Meldegesetz den Hauptwohnsitz in Freiburg. Er beendet hier sein Studium und kehrt für einige Zeit ins Elternhaus nach Sulzburg zurück. Da er hier in dieser kleinen Gemeinde bekannt ist, hält es keiner für nötig, den Zuzug amtlich zu erfassen. Die kleine Gemeinde hat einen Einwohner zu wenig, Freiburg einen zu viel. Findet dieser ehemalige Student in Hamburg ein Arbeitsplatz, so gibt er als bisherigen Wohnort Sulzburg an. Dort wird die Einwohnerzahl erniedrigt, in Hamburg erhöht. Es bleibt dabei: Die kleine Gemeinde hat einen Einwohner zu wenig, Freiburg einen zu viel.
Das statistische Amt der Stadt Freiburg geht solchen Fällen nach und kommt so zu niedrigeren Einwohnerzahlen. Andererseits ist es für Freiburg nicht schlecht, wenn im Landesamt 14 000 mehr Einwohner registriert sind. Denn pro Einwohner gibt es 1000 DM Ausgleichsmittel, das bringt immerhin 14 Millionen Mark in den Stadtsäckel.
"Erfahrungsgemäß sind es zumeist kleinere und mittlere Gemeinden, die das Statistische Landesamt darauf hinweisen, dass die von ihnen gemäß Melderegister ermittelte Einwohnerzahl höher liegt, als von der amtlichen Fortschreibung ausgewiesen. ... Im Zuge des Berichtigungsverfahrens ergibt sich meist eine Korrektur der amtlichen Bevölkerungszahl der ‘mahnenden’ Gemeinde nach oben." teilt der Präsident des Statistischen Landesamtes in einem offenen Brief an die Gemeinden mit. Damit ist klar: Da begünstigte Gemeinden wie Freiburg nicht mahnen, bei benachteiligten aber nachgebessert wird, ist die offiziell angegebene Einwohnerzahl in Baden-Württemberg und in jedem andern Bundesland und in der BRD zu hoch. Nach Volkszählungen müssen deshalb die Zahlen immer nach unten korrigiert werden, in Freiburg z.B. von 186 156 am 1.1.1987 auf 178 672 am 25.5.87 (minus 4%). Aber auch bei Volkszählungen rechnet man erfahrungsgemäß mit Fehlern von 1% bis 3%.
Bei Wasseruhren schreibt der Gesetzgeber eine Toleranz von max. ±10% vor. So kam es, dass im Jahre 1994 in einen Hochbehälter in Sulzburg 206 000 m³ Wasser hinein liefen (6 Wasseruhren), aber 218 000 m³ (eine Wasseruhr) hinaus! In einem Sechsfamilienhaus in Sulzburg zeigt die (eine) Wasseruhr, die den Gesamtverbrauch misst, immer mehr an, als sich aus der Addition des Verbrauchsmessung der sechs Uhren für die sechs Parteien ergibt. Ein Wasserverlust auf dem kurzen Leitungsweg ist ausgeschlossen. Was soll man nun davon halten, wenn der durchschnittliche Wasserverbrauch des Bundesbürgers mit 148 l pro Tag angegeben wird?
6. Welche Definition steckt hinter den Zahlen?
Italien hat 1987 erstmals England im Bruttosozialprodukt überholt und lag hinter USA, Japan, UdSSR, BRD und Frankreich erstmals an sechster Stelle. Dieser Tag ging als "Il sorpasso" <sorpassare = überholen> in die Geschichtsbücher Italiens ein und hob dort das Nationalbewußtsein, während er das der Engländer beschädigte. Was war passiert? Hatte man in Italien Gold gefunden? Hatten sie in die Hände gespuckt und das Bruttosozialprodukt gesteigert? Nein, man vergisst eines oft, wenn man exakte Zahlen vorgesetzt bekommt. Die Frage, welche Definition steckt dahinter. Das einzige, was sich geändert hatte, war die Definition des Bruttosozialprodukts. Während vorher - wie noch heute in Deutschland und vielen Ländern üblich - Schwarzarbeit u.ä. unberücksichtigt bleibt, hatte man nun in Italien die gesamte Schattenwirtschaft mit 5% im Bruttosozialprodukt angesetzt und es so um 5% gesteigert!
Heute schätzt man die Zahl der Analphabeten in der gesamten Bundesrepublik auf zwei bis drei Million, nach der letzten Statistik des Kaiserreichs, in der diese Zahl noch aufgeführt wurde (1912), gab es nur vier bis acht tausend Analphabeten. Wie ist das möglich?
Nun, ein Alphabet sollte heute u. a. einen einfachen Text sinnentnehmend lesen und ihn dann unter Berücksichtigung der wesentlichen Regeln der Schriftsprache schriftlich wiedergeben können. 1912 galt dagegen nur der als Analphabet, der seinen Namen nicht schreiben konnte. Denn die Zahlen des Kaiserreichs basieren auf Einträgen in Heiratsurkunden und Rekrutierung von Soldaten. Und es wurden nur die als Analphabeten gezählt, die mit XXX unterschrieben. Sollte man allerdings von einem Alphabeten verlangen, dass er seinen Steuerbescheid lesen können, dann - so schreibt Peek (1995) - wäre die Analphabetenrate wohl 99,9%.
Nach einer Zeitungsmeldung beherrscht ein Mathematikprofessor auch nur 5% der Mathematik. Ja, wie will man das denn messen? Wieviel Prozent der Mathematik macht denn die Differentialrechnung aus? Wer will das wie entscheiden? Wieviel weiß einer, der begriffen hat, was ein Grenzprozess bedeutet? Diese Zahl tagt nur zur Beruhigung frustrierter Mathelehrer, und das auch nur an lauen Sommerabenden.
7. Und was machen wir in der Schule?
Dazu nur ein Beispiel, stellvertretend für viele, die wir alle kennen.
Wir alle kennen Aufgaben, wie sie etwa Vollrath (1978) zitiert: "Eine 5 m³-Ladung Kies wiegt 10 t. Wieviel m³ Kies wird bei einer Ladung von 1,5 t transportiert?" Er stellt fest "Darüber hinaus suggerieren die Zahlenangaben fehlerfreie Messergebnisse."

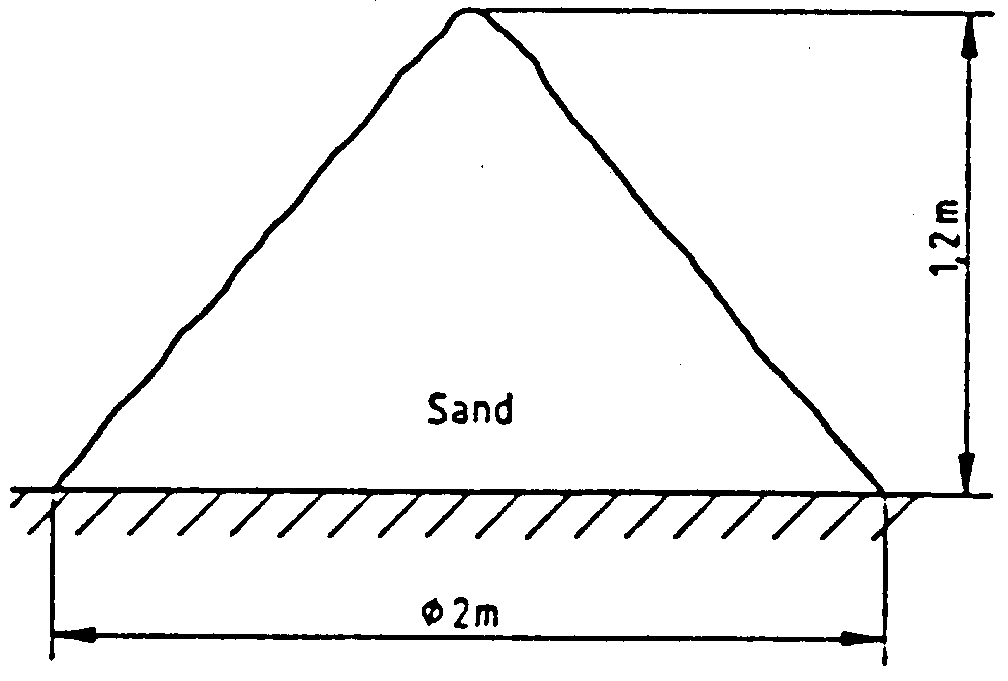
Diesen Artikel kennen die Autoren einer Prüfungsaufgabe des BVJs (Baden-Württemberg) des Jahres 1997 offensichtlich nicht. Sie verlangen, daß das Volumen und die Masse des kegelförmigen Sandhaufens (vgl. Abb.) zu berechnen. Obwohl der Rand des Sandhaufens nicht gradlinig gezeichnet ist und jeder die Ungenauigkeit sieht, wurde im Lösungsvorschlag das Volumen mit 1,256 m³ angegeben.
Woher kommen die Genauigkeit, die Stellen hinter dem Komma? Nun, eine Stelle von der Höhe 1,2 und zwei von ![]() , für das 3,14 eingesetzt wurde. Würde man
, für das 3,14 eingesetzt wurde. Würde man ![]() mit 10 000 Stellen angeben, hätte das Volumen des Sandhaufens auch 10 000 Stellen hinter dem Komma. (Ich weiß, genau 10001 Stellen.)
mit 10 000 Stellen angeben, hätte das Volumen des Sandhaufens auch 10 000 Stellen hinter dem Komma. (Ich weiß, genau 10001 Stellen.)
Dies habe ich so ironisch hingeschrieben. Und dann guck ich in den Lösungsvorschlag und trau meinen Augen nicht: Da haben doch die Ersteller genau das gemacht!! Bei der Berechnung der Masse (1 kg pro 1dm³) schreiben sie zwar zunächst 1256 dm³·1,5 kg/dm³ hin, kommen dann aber auf 1884,956 kg, was sie großzügig auf 1885 kg gerunden!
Übrigens - schüttet jemand einen Eimer Wasser auf den Sand, so nimmt dieser ihn auf und ist um 10 kg schwerer! Alleine durch Feuchtigkeitsschankungen ergeben größere Gewichtsunterschied als die Musterlösung suggeriert.
8. Vorschläge
Wie und in welcher Genauigkeit sollte man nun Zahlen angeben?
Hier hilft der Begriff der signifikante Ziffer. Die Zahl 1 321 900 000 (Wasser der Weltmeere) hat fünf, die Zahl 0,000 345 drei signifikante Ziffern, denn die folgenden bzw. führenden Nullen dienen nur der Festlegung der Größenordnung. Entsprechend hat die Zahl der Bundesbeschäftigten von 550 000 nur zwei signifikante Ziffern. Will man dagegen behaupten, daß es 550 0000 und nicht 551 000 sind, hätte diese Zahl drei signifikante Ziffern. In diesem Fall empfiehlt sich die Schreibweise 550·10³, bei der alle signifikanten Ziffern aufgeführt werden, führende oder folgende Nullen aber durch die Exponentialschreibweise entfallen.
Auf Gauss geht die Konvention zurück, daß man entweder den Fehler explizit angibt. Ein Literaturwert der Gravitationskonstante ist z.B. ![]() m³/kg s², der relativer Fehler beträgt also 0,0127%. Oder man schreibt nur so viele signifikant Ziffern, daß der Fehler maximal die Hälfte der letzten signifikanten Zahl ausmacht. Bei 1 321 900 000 (Wasser der Weltmeere) wäre dies ±50 000, also nur ein relativer Fehler von 5 : 132190 oder rund(!) 0,004%. Glaubt wirklich jemand, dass man die Wassermenge der Weltmeere genauer messen kann als die Gravitationskonstante, (die zugegebenermaßen eine der ungenausten Naturkonstanten ist).
m³/kg s², der relativer Fehler beträgt also 0,0127%. Oder man schreibt nur so viele signifikant Ziffern, daß der Fehler maximal die Hälfte der letzten signifikanten Zahl ausmacht. Bei 1 321 900 000 (Wasser der Weltmeere) wäre dies ±50 000, also nur ein relativer Fehler von 5 : 132190 oder rund(!) 0,004%. Glaubt wirklich jemand, dass man die Wassermenge der Weltmeere genauer messen kann als die Gravitationskonstante, (die zugegebenermaßen eine der ungenausten Naturkonstanten ist).
Aufgrund der Anfangsziffer und der Anzahl der signifikanten Ziffer kann man den nach der Vorschrift von Gauss prozentualen Fehler (runden!) angeben, wie hier in der Tabelle dargestellt. Hat man z.B. nur die eine signifikante Ziffer 2, dann bedeutet das also 2 ± 0,5, und wegen 0,5 : 2 = 0,25 ist der relative Fehler 25%.
|
Anzahl der signifikanten Ziffern
|
|||
|
erste 1 |
50 |
3 |
0,3 |
|
signifi- 2 |
25 |
2 |
0,2 |
|
kante 3 |
17 |
1 |
0,1 |
|
Ziffer 4 |
13 |
1 |
0,1 |
|
5 |
10 |
0,9 |
0,09 |
|
6 |
8 |
0,7 |
0,07 |
|
7 |
7 |
0,7 |
0,07 |
|
8 |
6 |
0,6 |
0,06 |
|
9 |
6 |
0,5 |
0,05 |
Relativer Fehler in %
Man tut sich relativ leicht, diesen prozentualen Fehler zu schätzen. Daraus ergibt sich nun umgekehrt, wieviel signifikante Ziffern man verwenden sollte.
Das ist vielleicht zu schwer für das BVJ und die Berechnung am Sandhaufen (s.o.). Aber ich kann mir vorstellen, wie mein Kollege Stenger, der dort unterrichtet, die Frage stellt: "Na, schätz mal, um wieviel Prozent das Volumen des Sandhaufens schwanken kann! - - Hm, 5%? Ein bisschen wenig, findest Du nicht?" Wenn man sich dann auf 10% oder 20% geeinigt hat, können die Schüler diese Schwankung um den Wert 1,256 m³ mit 0,1256 m³ oder 0,2512 m³ angeben und werden feststellen, dass die Angabe 1,3 m³ schon zu genau ist. Und sie erfahren, dass mit dem Sandhaufen ein Auto mit einer zulässigen Zuladung von 2-Tonnen u.U. schon überladen ist.
Der Kollege Bardy schlägt an dieser Stelle das "Doppelt-Rechnen" vor. Gibt man nur die signifikanten Ziffern an, hier etwa die Höhe mit 1,2 m, den Durchmesser mit 2,0 m und die Dichte mit 1,5 kg/dm³, so ergeben sich nach der Regel von Gauss die Bereiche 1,2 m ±0,05 m, 2,0 m ±0,05 m und 1,5 kg/dm³ ±0,05 kg/dm³. Für die Masse des Sandhaufens erhält man nun maximal 1/3 · (3,14 · 1,025² · 1,25) · 1,55 = 2,13 ... und minimal 1/3 · (3,14 · 0,975² · 1,15) · 1,45 = 1,65 ... , woraus man ersieht, wie gewagt die Angabe von rund 1,9 t ist.
Lit:
Bericht der Bundesregierung: Zur Bekämpfung des Analphabetismus in der Bundesrepublik Deutschland 19/93. Bonn 1993, Drucksache 12/5821
Krämer, W. (1991): So lügt man mit Statistik, Reihe Campus, Frankfurt, New York
Laussermayer, R. (1996): Rechnen mit zwei signifikanten Ziffern (Dis-positionsmathematik). In: Bardy, Danckwerts, Schornstein (Hrsg.): Materialen für einen realitätsbeuognenen Mathematikunterricht, Band 3 der ISTRON-Reihe, Franzbecker, Bad Salzdetfurth
Morgenstern, O. (1973): On the Accuracy of Economic Observations. Princeton University Press, 2. Aufl., Princeton
Peek, R. (1995): Funktionaler Analphabetismus in modernen Industriestaaten. In: Bertelsmann Briefe, H. 133, s. 68 - 70
Vollrath, H-J. (1978):Schülerversuche zum Funktionsbegriff. In: MU4/78, S. 90-101
Staatliches Seminar für Schulpädagogik (Gymnasien) Rottweil (1993): Beiträge zur Lehrerfortbildung, Band 22, Wasser und Mathematik. Rottweil
Vereinigung Deutscher Gewässerschutz (1995): Schriftenreihe der, Band 37, Naturstoff Wasser, 3. Auflage, Bonn