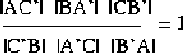

Next: Schnitte (M. Doorman/H. Schuhmann
Up: Beurteilung einiger Programme
Previous: Beurteilung einiger Programme
Euklid ist ein sogenanntes ,,dynamisches Programm``. Es erlaubt zunächst
das Konstruieren wie mit Zirkel und Lineal. Des weiteren stehen bereits
einige Makros wie Mittelsenkrechte, Winkelhalbierende, Parallele etc.
zur Verfügung. Es können aber auch eigene Makros erstellt werden.
Dazu legt man lediglich die Ausgangskonfiguration fest, definiert
die Zielkonfiguration, indem man die Konstruktion einmal durchführt,
gibt dem Makro einen Namen, und ab sofort steht es zur Verfügung.
Wie alle dynamischen Programme bietet Euklid den grossen Vorteil des
Zugmodus: Hat man eine Zeichnung erstellt, so kann man jeden (freien ) Punkt ,,anfassen`` (der Mauszeiger verwandelt sich in eine Beißzange)
und ihn beliebig über den Bildschirm ziehen. Alle Konstruktionen werden
ständig neu berechnet, die Zeichnung verändert sich dynamisch. Des
weiteren steht ein Programmpunkt ,,Messen und Rechnen`` zur Verfügung,
der es erlaubt, auf einfache Weise Winkel und Abstände zu messen.
Weiterhin können Rechenausdrücke eingegeben werden, die einzelne Objekte
mit den vier Grundrechenarten verknüpfen, und während des Ziehens
im Zugmodus überwacht werden.
) Punkt ,,anfassen`` (der Mauszeiger verwandelt sich in eine Beißzange)
und ihn beliebig über den Bildschirm ziehen. Alle Konstruktionen werden
ständig neu berechnet, die Zeichnung verändert sich dynamisch. Des
weiteren steht ein Programmpunkt ,,Messen und Rechnen`` zur Verfügung,
der es erlaubt, auf einfache Weise Winkel und Abstände zu messen.
Weiterhin können Rechenausdrücke eingegeben werden, die einzelne Objekte
mit den vier Grundrechenarten verknüpfen, und während des Ziehens
im Zugmodus überwacht werden.
- Beispiel
- (siehe Abbildung 1) : Es sei ein Punkt im Innern eines
beliebigen Dreiecks . Von jedem Eckpunkt des Dreiecks aus wird eine
Gerade durch gezeichnet; diese schneidet die gegenüberliegende Dreiecksseite
in (bzw. ) Dann gilt der ,,Satz von Ceva``:
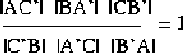
Indem der Schüler sich die entsprechende Situation konstruiert, und
diesen Überwachungsausdruck eingegeben hat, kann er sich durch das
Ziehen der Eckpunkte davon überzeugen, dass die Aussage stimmt: Das
Ausgabe-Fenster zeigt ihm das unveränderte Ergebnis der Berechnung.
Dies ersetzt natürlich keinen Beweis, aber es zeigt doch, dass es
eine Gesetzmäßigkeit gibt, die es sich vielleicht zu beweisen lohnt.
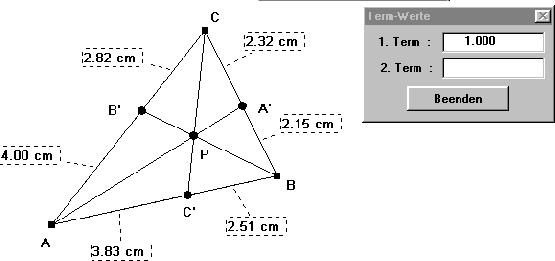
Abbildung 1: Satz von Ceva. Die Strecken wurden ausgemessen, der Rechenausdruck
eingegeben, und das Ergebnis ist abzulesen. Der Satz wurde verifiziert.
Ein weiteres sinnvolles Werkzeug ist die Ortslinienfunktion. Weist
man das Programm an, für einen Punkt (oder auch mehrere Punkte) die
Ortslinie zu zeichnen, so hinterläßt dieser Punkt beim Ziehen anderer
Punkte eine Spur seiner Bewegung, die Ortslinie. Abbildung 2 zeigt
beispielsweise die Entstehung einer Ellipse.
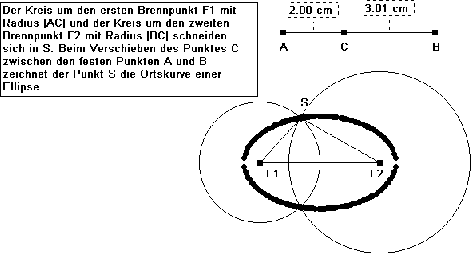
Abbildung 2: Zur Entstehung einer Ellipse mit Hilfe der Ortslinienfunktion.
Euklid ist in der Lage, einen vollständigen Konstruktionstext auszugeben.
Dieser Konstruktionstext ist allerdings sehr umfangreich, da selbst
das Setzen eines einzigen Punktes aufgeführt wird. Der Konstruktionstext
kann aber nachträglich bearbeitet werden. Ebenso ist es möglich, mithilfe
der Funktion ,,Rückblende`` die Konstruktion Schritt für Schritt noch
einmal vorzuführen. So kann der Lehrer oder die Lehrerin komplexere
Konstruktionen, oder Lösungen schwieriger Aufgaben zu Hause vorbereiten,
und den Schülern und Schülerinnen vorführen. Euklid ist in seiner
Handhabung äußerst einfach. Die Oberfläche ist übersichtlich gestaltet,
und verfügt über ein selbsterklärendes Hilfesystem. Zum Test baten
wir einen Studenten, der noch nie mit einem solchen Programm gearbeitet
hat, eine Konstruktion durchzuführen. Dies gelang ohne Probleme in
recht kurzer Zeit. Hier nochmal alle Vor- & Nachteile von Euklid
auf einen Blick:
Vorteile:
- Dynamisches Verändern der Zeichnung mittels Zugmodus.
- Erstellen eigener Makros.
- Ortslinienfunktion.
- Automatisches Erstellen des Konstruktionstextes.
- Intuitive Bedienung; es sind keine Vorkenntnisse nötig.
Nachteile:
- Nachträglich abgeänderter Konstruktionstext kann nicht gespeichert
werden.
- Bei längeren Überwachungsausdrücken erweist sich die Termeingabe als
etwas unübersichtlich.
Euklid wird als Shareware vertrieben. Eine Demo-Version kann über
das Internet heruntergeladen werden. Einen Link finden Sie auf unserer
Homepage (s. Kap. 4).


Next: Schnitte (M. Doorman/H. Schuhmann
Up: Beurteilung einiger Programme
Previous: Beurteilung einiger Programme
Wed Oct 8 22:30:48 MEST 1997
 ) Punkt ,,anfassen`` (der Mauszeiger verwandelt sich in eine Beißzange)
und ihn beliebig über den Bildschirm ziehen. Alle Konstruktionen werden
ständig neu berechnet, die Zeichnung verändert sich dynamisch. Des
weiteren steht ein Programmpunkt ,,Messen und Rechnen`` zur Verfügung,
der es erlaubt, auf einfache Weise Winkel und Abstände zu messen.
Weiterhin können Rechenausdrücke eingegeben werden, die einzelne Objekte
mit den vier Grundrechenarten verknüpfen, und während des Ziehens
im Zugmodus überwacht werden.
) Punkt ,,anfassen`` (der Mauszeiger verwandelt sich in eine Beißzange)
und ihn beliebig über den Bildschirm ziehen. Alle Konstruktionen werden
ständig neu berechnet, die Zeichnung verändert sich dynamisch. Des
weiteren steht ein Programmpunkt ,,Messen und Rechnen`` zur Verfügung,
der es erlaubt, auf einfache Weise Winkel und Abstände zu messen.
Weiterhin können Rechenausdrücke eingegeben werden, die einzelne Objekte
mit den vier Grundrechenarten verknüpfen, und während des Ziehens
im Zugmodus überwacht werden.