Wintersemester 2014: Proseminar Symmetrische Funktionen

Prof. Dr. Katrin Wendland
PD Emanuel Scheidegger

Seminar

• Wann und wo:

  Di 14 - 16, SR 127

• Thema:

  Ein symmetrisches Polynom ist ein Polynom in $n$ Variablen, welches invariant unter Permutationen der Variablen ist. Symmetrische Polynome treten natürlich in der Beziehung zwischen den Nullstellen eines Polynoms in einer Variable und seinen Koeffizienten auf. Nach dem Satz von Vieta sind die Koeffizienten dieses Polynoms wiederum Polynome in den Nullstellen, wobei die Reihenfolge der Nullstellen keine Rolle spielt. Dies führt auf die elementar-symmetrischen Polynome, die eine fundamentale Rolle spielen, da alle symmetrischen Polynome durch Linearkombinationen von elementar-symmetrischen ausgedrückt werden können.

  Unabhängig davon bilden die symmetrischen Polynome interessante Strukturen. Wir werden weitere ausgezeichnete symmetrische Polynome, wie z.B. die Schurpolynome kennenlernen. Deren Multiplikation kann mit Hilfe von Young-Tableaux grafisch dargestellt werden:

  

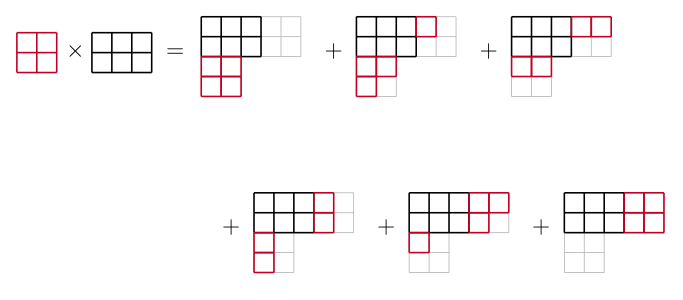
  Die Verallgemeinerung auf unendlich viele Variablen führt zum Ring der symmetrischen Funktionen, welcher eine zentrale Rolle in der Kombinatorik und in der Darstellungstheorie spielt.

Tutorium

• Emanuel Scheidegger, Sprechstunde: Mi 16 - 17, Raum 329

Vortragsliste

Literatur

• I.G. Macdonald, Symmetric Functions and Hall Polynomials, Oxford Science Publications, 2nd ed., 1995
• W. Fulton, J. Harris, Representation theory. A first course. Springer-Verlag, 1991