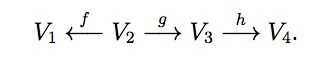Sommersemester 2020: Proseminar Darstellungstheorie von Köchern

Prof. Dr. Katrin Wendland
Dr. Severin Barmeier

Wann und wo: Laut Vorgabe der Leitung der Universität Freiburg zur Durchführung des Vorlesungsbetriebes im Sommersemester 2020 beginnt das Proseminar in der Woche vom 11. Mai 2020 und endet in der Woche vom 31. Juli 2020. Die Termine der einzelnen Vorträge verschieben sich entsprechend.
Auch kann das Proseminar nur digital durchgeführt werden. Wir planen, dass die Vorträge live an alle Teilnehmerinnen und Teilnehmer übertragen werden, und zwar

dienstags, 12:00 - 14:00 Uhr

Die Zugangsdaten erhalten Sie über den e-Mail Verteiler des Seminares. Eventuell werden auch Aufzeichnungen hinterher ins Netz gestellt; auch hierzu erhalten Sie alle weiteren Informationen über den e-Mail Verteiler des Seminares. Wir bitten um Ihr Verständnis, dass wir aufgrund der sich ständig ändernden Situation noch keine endgültigen Angaben machen können.

Vorbesprechung: Di 11.02.2020, 14:15, SR 119, Ernst-Zermelo-Str. 1
Um teilzunehmen, kommen Sie bitte in die Vorbesprechung des Proseminars; eine Teilnehmerliste wird nicht vorab ausliegen.

Thema:
Die lineare Algebra befasst sich mit linearen Abbildung zwischen Vektorräumen. Eine lineare Abbildung f: V → W zwischen zwei Vektorräumen V, W kann man nun grafisch als "Pfeil" zwischen zwei "Knotenpunkten" darstellen: • → •. Dieses Bild lässt sich verallgemeinern zu sogenannten "Köchern" (engl. quiver) - bestehend eben aus einer Ansammlung von Pfeilen, z.B.

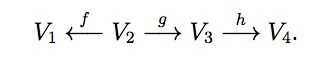
Eine Darstellung von einem Köcher ist nun gegeben durch die Wahl eines Vektorraums an jedem Knotenpunkt und eine lineare Abbildung für jeden Pfeil, z.B. für den linken Köcher Um in die Theorie der Köcherdarstellungen einzusteigen, benötigt man tatsächlich nur Vorkenntnisse aus der linearen Algebra. Umso erstaunlicher ist es, dass Köcherdarstellungen nicht nur in der Darstellungstheorie, sondern auch in der algebraischen Geometrie bis hin zur mathematischen Physik weitreichende Anwendungen haben.
In diesem Seminar wollen wir die Darstellungstheorie von Köchern Schritt für Schritt entwickeln. Am Ende des Seminars behandeln wir den Satz von Gabriel über "darstellungs-endliche" Köcher, der beschreibt für welche Köcher sich beliebige Darstellungen aus endlich vielen unzerlegbaren Bausteinen zusammensetzen lassen. Erstaunlicherweise gibt es auch hier eine Verbindung zu anderen Teilen der Mathematik, nämlich zu Dynkin-Diagrammen, die in der Klassifizierung von Lie-Algebren eine fundamentale Rolle spielen.
Die Theorie der Köcherdarstellungen ist ein ausgezeichnetes Thema, um abstraktere Konzepte aus der Algebra (assoziative Algebren, Kategorien von Moduln, Anfänge der homologischen Algebra) kennenzulernen und dank der grafischen / diagrammatischen Herangehensweise ganz konkret zu veranschaulichen.

Literatur:
Falls ein Link gesetzt ist, dann führt dieser auf eine Webseite, von der aus dem Universitätsnetz die jeweilige Referenz zugänglich ist. Falls kein Link gesetzt ist, finden Sie die Referenz in der Bibliothek des Mathematischen Institutes Freiburg.

• R. Schiffler, Quiver representations, CMS Books in Mathematics, Springer, 2014
• A. Kirillov Jr., Quiver representations and quiver varieties, Graduate Studies in Mathematics 174, AMS, 2016

Vortragsprogamm: hier

Tutorium: Severin Barmeier